题目内容
已知数列{an}满足: (其中常数λ>0,n∈N*).
(其中常数λ>0,n∈N*).
(1)求数列{an}的通项公式;
(2)当λ=4时,是否存在互不相同的正整数r,s,t,使得ar,as,at成等比数列?若存在,给出r,s,t满足的条件;若不存在,说明理由;
(3)设Sn为数列{an}的前n项和.若对任意n∈N*,都有(1-λ)Sn+λan≥2λn恒成立,求实数λ的取值范围.
 (其中常数λ>0,n∈N*).
(其中常数λ>0,n∈N*).(1)求数列{an}的通项公式;
(2)当λ=4时,是否存在互不相同的正整数r,s,t,使得ar,as,at成等比数列?若存在,给出r,s,t满足的条件;若不存在,说明理由;
(3)设Sn为数列{an}的前n项和.若对任意n∈N*,都有(1-λ)Sn+λan≥2λn恒成立,求实数λ的取值范围.
(1)an=(2n+1)·λn-1 (n∈N*).(2)不存在这样的正整数r,s,t,使得ar,as,at成等比数列.(3)当0<λ<1时,结论成立.
本试题主要是考查了数列的通项公式以及数列的求和、和不等式的成立的证明综合运用。
(1)根据已知条件可知利用前n项和与通项公式之间的关系得到通项公式。
(2)因为当λ=4时,an=(2n+1)·4n-1.
若存在ar,as,at成等比数列,则[(2r+1)·4r-1] [(2t+1)·4t-1]=(2s+1)2 ·42s-2.
整理得(2r+1) (2t+1) 4 r+t -2s=(2s+1)2,可以判定为等比数列。
(3)因为Sn=3+5λ+7λ2+…+(2n+1)λn-1.,需要对于参数λ分情况讨论得到和式的求解,以及不等式的证明。
(1)根据已知条件可知利用前n项和与通项公式之间的关系得到通项公式。
(2)因为当λ=4时,an=(2n+1)·4n-1.
若存在ar,as,at成等比数列,则[(2r+1)·4r-1] [(2t+1)·4t-1]=(2s+1)2 ·42s-2.
整理得(2r+1) (2t+1) 4 r+t -2s=(2s+1)2,可以判定为等比数列。
(3)因为Sn=3+5λ+7λ2+…+(2n+1)λn-1.,需要对于参数λ分情况讨论得到和式的求解,以及不等式的证明。

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
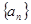 的前
的前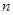 项和为
项和为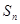 ,且满足
,且满足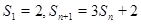
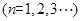 .
.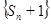 为等比数列;
为等比数列;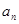 ;
;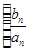 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列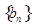 的前
的前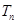 .
. 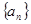 中,
中,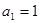 ,
,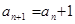 ,则
,则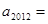
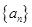 ,
,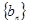 满足:
满足: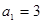 ,当
,当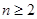 时,
时,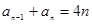 ;对于任意的正整数
;对于任意的正整数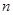 ,
,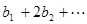
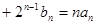 .设数列
.设数列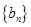 的前
的前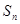 .
.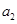 、
、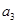 ,并求数列
,并求数列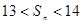 的正整数
的正整数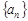 中,
中,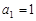 ,
,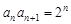
 ,则数列
,则数列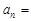 .
. 中,
中,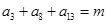 ,其前n项
,其前n项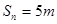 ,则n=
,则n= 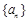 中,已知
中,已知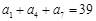 ,
,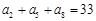 ,则
,则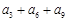 的值是( )
的值是( )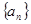 的前n项和
的前n项和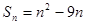 ,第k项满足
,第k项满足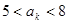 ,则k=_______
,则k=_______