题目内容
11.函数f(x)=3sin(x+10°)+5sin(x+70°)的最大值是( )| A. | 7 | B. | $\sqrt{34}$ | C. | 4 | D. | 8 |
分析 由和差角公式和辅助角公式可得f(x)=7sin(x+10°+φ),可得函数最大值为7
解答 解:化简可得f(x)=3sin(x+10°)+5sin(x+70°)
=3sin(x+10°)+5sin[(x+10°)+60°]
=3sin(x+10°)+5sin(x+10°)cos60°+5cos(x+10°)sin60°
=$\frac{11}{2}$sin(x+10°)+$\frac{5\sqrt{3}}{2}$cos(x+10°)
=$\sqrt{(\frac{11}{2})^{2}+(\frac{5\sqrt{3}}{2})^{2}}$sin(x+10°+φ),其中tanφ=$\frac{5\sqrt{3}}{11}$,
=7sin(x+10°+φ)≤7
∴所求函数的最大值为:7
故选A.
点评 本题考查三角函数的最值问题,涉及辅助角公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
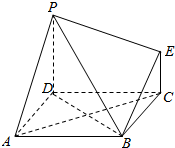 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且