题目内容
1.已知函数y=f(x)是定义域为R偶函数,当x≥0时,f(x)=$\left\{\begin{array}{l}{-\frac{{x}^{2}}{2},0≤x≤2}\\{\frac{x}{1-x},x>2}\end{array}\right.$,若函数f(x)在(t,t+2)上的值域是$(-\frac{3}{2},0]$,则实数t的值的集合为{-$\sqrt{3}$,$\sqrt{3}$-2}.分析 根据函数奇偶性的性质求出函数f(x)的表达式,利用数形结合进行求解即可.
解答 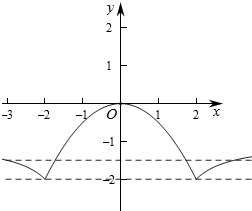 解:∵函数y=f(x)是定义域为R偶函数,
解:∵函数y=f(x)是定义域为R偶函数,
∴若-2≤x≤0,则0≤-x≤2,则f(-x)=$-\frac{{x}^{2}}{2}$=f(x),
即当-2≤x≤0,f(x)=$-\frac{{x}^{2}}{2}$,
若x<-2,则-x>2,则f(-x)=$\frac{-x}{1+x}$=f(x),
即当x<-2,f(x)=$-\frac{x}{1+x}$,
作出函数f(x)的图象如图:
当x=0时,f(x)=0,
当x=2时,f(2)=-2,
由$-\frac{{x}^{2}}{2}$=-$\frac{3}{2}$得x2=3,x=±$\sqrt{3}$,
由$\frac{x}{1-x}$=-$\frac{3}{2}$得x=3,
由$\frac{-x}{1+x}$=-$\frac{3}{2}$得x=-3,
若函数的值域为$(-\frac{3}{2},0]$,
则t<0<t+2即-2<t<0,
当t=-$\sqrt{3}$时,f(t)=-$\frac{3}{2}$,此时t+2=2-$\sqrt{3}$,
∵0<2-$\sqrt{3}$<$\sqrt{3}$,
∴满足函数的值域为$(-\frac{3}{2},0]$,
若t+2=$\sqrt{3}$时,即f(t+2)=-$\frac{3}{2}$,此时t=$\sqrt{3}$-2,
∵-$\sqrt{3}$<$\sqrt{3}$-2<0,
∴满足函数的值域为$(-\frac{3}{2},0]$,
综上t=-$\sqrt{3}$或$\sqrt{3}$-2,
故答案为:{-$\sqrt{3}$,$\sqrt{3}$-2}
点评 本题主要考查分段函数的应用,利用函数奇偶性的性质求出函数的解析式,利用数形结合是解决本题的关键.综合性较强.

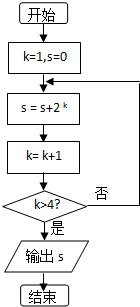 执行如图所示的程序框图,则输出s的值为( )
执行如图所示的程序框图,则输出s的值为( )| A. | 30 | B. | 31 | C. | 62 | D. | 63 |
| A. | 方程x2+bx+a=0至多一个实根 | B. | 方程x2+bx+a=0有实根 | ||
| C. | 方程x2+bx+a=0至多有两个实根 | D. | 方程x2+bx+a=0恰好有两个实根 |
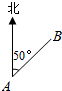 某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.
某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.