��Ŀ����
7������ij������ҵ2008����2014�����۶�y����λ����Ԫ�����������±���ʾ��| ��� | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| ����t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| ���۶�y | 27 | 31 | 35 | 41 | 49 | 56 | 62 |
��2����y����t�����Իع鷽�̣�������ݱ�����λС����
��3����������ع鷽�̣�˵��2008����2014��ô�����ҵ���۶�ı仯�������Ԥ�����ҵ2015������۶������ݱ�����λС����
�����ع�ֱ�ߵ�б�ʵ���С���˷����ƹ�ʽ��b=$\frac{\sum_{i=1}^{n}��{t}_{i}-\overline{t}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{t}_{i}-\overline{t}��^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}$��
���� ��1���и���������ϵ������������ݶ�Ӧ�ĵ㣬�ɵ���ݴ��������۶��ɢ��ͼ��
��2���������������ݣ�������С���˷��ɵú����ݱ��ƽ�����������ݱ�Ļ��ĺͣ������ƽ���ͣ����빫ʽ���b��ֵ�������a��ֵ��д�����Իع鷽�̣�
��3��������һ�����������Իع鷽�̣�����������t��ֵ��Ԥ��õ���2015������۶
��� �⣺��1����ݴ��������۶��ɢ��ͼ������ʾ��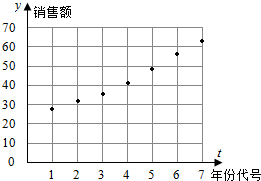
��2������֪�е����ݿɵã�
$\overline{t}$=$\frac{1}{7}$��1+2+3+4+5+6+7��=4��
$\overline{y}$=$\frac{1}{7}$��27+31+35+41+49+56+62��=43��
$\sum _{i=1}^{7}{t}_{i}{y}_{i}$=1373��$\sum _{i=1}^{7}{{t}_{i}}^{2}$=140��
��$\hat{b}$=$\frac{\sum _{i=1}^{7}{t}_{i}{y}_{i}-7\overline{t}\overline{y}}{\sum _{i=1}^{7}{{t}_{i}}^{2}-7{\overline{t}}^{2}}$=$\frac{1373-1204}{140-112}$=$\frac{169}{28}$��6.04��
��$\hat{a}$=$\overline{y}$-6.04$\overline{t}$=18.84��
��y����t�����Իع鷽��$\hat{y}$=6.04x+18.84��
��3��2015�����ݴ���Ϊ8��
��t=8ʱ��$\hat{y}$=6.04��8+18.84=67.16��
��Ԥ�����ҵ2015������۶�ԼΪ67.16��Ԫ
���� ���⿼�����Իع������Ӧ�ã��������Ĺؼ���������С���˷������������Իع鷽�̵�ϵ��������������Ŀ���Եıر�������������һ�������⣮

| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{5}$ | C�� | $\frac{1}{7}$ | D�� | $\frac{1}{9}$ |
| A�� | $��{1��1+\frac{{\sqrt{2}}}{2}}��$ | B�� | $��{1+\frac{{\sqrt{2}}}{2}��+��}��$ | C�� | $��{1��1+\sqrt{2}}��$ | D�� | $��{1+\sqrt{2}��+��}��$ |
| A�� | ������x��2������x2��4 | B�� | ��x��2������x2��4 | ||
| C�� | ����x��2��ʹx2��4 | D�� | ����x��2��ʹx2��4 |
| A�� | {��1��1��} | B�� | {��-1��1������1��1��} | C�� | $[{\frac{1}{2}��+��}��$ | D�� | $[{\frac{{\sqrt{2}}}{2}��+��}��$ |
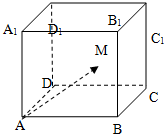 ��ͼ�����ⳤΪ2��������ABCD-A1B1C1D1�ڣ�����������棩��ȡһ��M����$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$��1�ĸ����ǣ�������
��ͼ�����ⳤΪ2��������ABCD-A1B1C1D1�ڣ�����������棩��ȡһ��M����$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$��1�ĸ����ǣ�������| A�� | $\frac{5}{6}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{4}$ |