题目内容
17.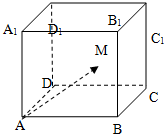 如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是( )
如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是( )| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 本题是几何概型问题,欲求点M满足则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率,先以A为原点建立空间直角坐标系,由数量积公式得出点M到平面ABCD的距离大于等于$\frac{1}{2}$,点M的轨迹是正方体的$\frac{3}{4}$,求出其体积,再根据几何概型概率公式结合正方体的体积的方法求解即可
解答 解:本题是几何概型问题,正方体的体积为V=8,
以A为原点建立空间直角坐标系,AB为x轴,AD为y轴,AA1为z轴.
那么A(0,0,0),A1(0,0,2)
设M(x,y,z),那么x,y,z∈[0,2]
∴$\overrightarrow{AM}$=(x,y,z),$\overrightarrow{A{A}_{1}}$=(0,0,2)
则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1,即2z≥1,z≥$\frac{1}{2}$.
即点M与平面ABCD的距离大于等于$\frac{1}{2}$,点M的轨迹是正方体的$\frac{3}{4}$,其体积为:V1=$\frac{3}{4}$,
则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率p为$\frac{3}{4}$;
故选:D.
点评 本小题主要考查几何概型、几何概型的应用、几何体的体积等基础知识,考查空间想象能力、化归与转化思想.属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
7.我市某大型企业2008年至2014年销售额y(单位:亿元)的数据如下表所示:
(1)在下表中,画出年份代号与销售额的散点图;
(2)求y关于t的线性回归方程,相关数据保留两位小数;
(3)利用所求回归方程,说出2008年至2014年该大型企业销售额的变化情况,并预测该企业2015年的销售额,相关数据保留两位小数.
附:回归直线的斜率的最小二乘法估计公式:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}$.
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 销售额y | 27 | 31 | 35 | 41 | 49 | 56 | 62 |

(2)求y关于t的线性回归方程,相关数据保留两位小数;
(3)利用所求回归方程,说出2008年至2014年该大型企业销售额的变化情况,并预测该企业2015年的销售额,相关数据保留两位小数.
附:回归直线的斜率的最小二乘法估计公式:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}$.
12.若不等式组$\left\{\begin{array}{l}x-y+2≥0\\ x-5y+10≤0\\ x+y-8≤0\end{array}\right.$所表示的平面区域存在点(x0,y0)使x0+ay0+2≤0成立,则实数a的取值范围是( )
| A. | a>1 | B. | a>-1 | C. | a≤1 | D. | a≤-1 |
9.设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值,若对于任意的x∈[0,3],都有f(x)<c2成立,则实数c的取值范围为( )
| A. | (-1,9) | B. | (-9,1) | C. | (-∞,-1)∪(9,+∞) | D. | (-∞,-9)∪(1,+∞) |
4.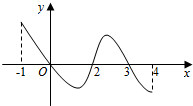 已知函数f(x)的定义域为[-1,4],部分对应值如表,
已知函数f(x)的定义域为[-1,4],部分对应值如表,
f(x)的导函数y=f′(x)的图象如图所示.当1<a<2时,函数y=f(x)-a的零点的个数为( )
 已知函数f(x)的定义域为[-1,4],部分对应值如表,
已知函数f(x)的定义域为[-1,4],部分对应值如表,| x | -1 | 0 | 2 | 3 | 4 |
| f(x) | 1 | 2 | 0 | 2 | 0 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |