题目内容
已知向量p=(an,2n),向量q=(2n+1,-an+1),n∈N*,向量p与q垂直,且a1=1.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=log2an+1,求数列{an·bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=log2an+1,求数列{an·bn}的前n项和Sn.
(1) an=2n-1 (2) an·bn=n·2n-1 Sn=1+(n-1)2n
解:(1)∵向量p与q垂直,
∴2nan+1-2n+1an=0,即2nan+1=2n+1an,
∴ =2,∴{an}是以1为首项, 2为公比的等比数列,∴an=2n-1.
=2,∴{an}是以1为首项, 2为公比的等比数列,∴an=2n-1.
(2)∵bn=log2an+1,∴bn=n,
∴an·bn=n·2n-1,
∴Sn=1+2·2+3·22+4·23+…+n·2n-1,①
∴2Sn=1·2+2·22+3·23+4·24+…+n·2n,②
①-②得,
-Sn=1+2+22+23+24+…+2n-1-n·2n
= -n·2n=(1-n)2n-1,
-n·2n=(1-n)2n-1,
∴Sn=1+(n-1)2n.
∴2nan+1-2n+1an=0,即2nan+1=2n+1an,
∴
 =2,∴{an}是以1为首项, 2为公比的等比数列,∴an=2n-1.
=2,∴{an}是以1为首项, 2为公比的等比数列,∴an=2n-1.(2)∵bn=log2an+1,∴bn=n,
∴an·bn=n·2n-1,
∴Sn=1+2·2+3·22+4·23+…+n·2n-1,①
∴2Sn=1·2+2·22+3·23+4·24+…+n·2n,②
①-②得,
-Sn=1+2+22+23+24+…+2n-1-n·2n
=
 -n·2n=(1-n)2n-1,
-n·2n=(1-n)2n-1,∴Sn=1+(n-1)2n.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
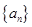 中,
中,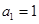 ,前
,前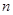 项和为
项和为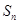 ,对任意
,对任意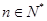 ,
,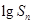 、
、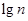 、
、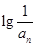 成等差数列.
成等差数列.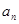 和
和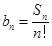 ,数列
,数列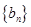 的前
的前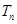 ,当
,当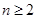 时,证明:
时,证明: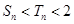 .
.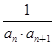 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn. 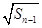 -Sn-1
-Sn-1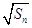 =2
=2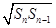 (n∈N*且n≥2),则a81=( )
(n∈N*且n≥2),则a81=( )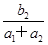 的值为________.
的值为________.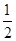 +
+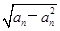 ,且a1=
,且a1=