题目内容
已知Sn是等比数列{an}的前n项和,S4,S2,S3成等差数列,且a2+a3+a4=-18.
(1)求数列{an}的通项公式;
(2)是否存在正整数n,使得Sn≥2 013?若存在,求出符合条件的所有n的集合;若不存在,说明理由.
(1)求数列{an}的通项公式;
(2)是否存在正整数n,使得Sn≥2 013?若存在,求出符合条件的所有n的集合;若不存在,说明理由.
(1) an=3×(-2)n-1 (2) 存在,{n|n=2k+1,k∈N,k≥5},理由见解析
解:(1)设数列{an}的公比为q,则a1≠0,q≠0.由题意得
 即
即
解得
故数列{an}的通项公式为an=3×(-2)n-1.
(2)由(1)有Sn= =1-(-2)n.
=1-(-2)n.
若存在n,使得Sn≥2 013,则1-(-2)n≥2 013,即(-2)n≤-2 012.
当n为偶数时,(-2)n>0,上式不成立;
当n为奇数时,(-2)n=-2n≤-2 012,
即2n≥2 012,则n≥11.
综上,存在符合条件的正整数n,且所有这样的n的集合为{n|n=2k+1,k∈N,k≥5}.
 即
即
解得

故数列{an}的通项公式为an=3×(-2)n-1.
(2)由(1)有Sn=
 =1-(-2)n.
=1-(-2)n.若存在n,使得Sn≥2 013,则1-(-2)n≥2 013,即(-2)n≤-2 012.
当n为偶数时,(-2)n>0,上式不成立;
当n为奇数时,(-2)n=-2n≤-2 012,
即2n≥2 012,则n≥11.
综上,存在符合条件的正整数n,且所有这样的n的集合为{n|n=2k+1,k∈N,k≥5}.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
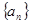 是等差数列,且
是等差数列,且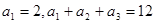
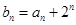 ,求数列
,求数列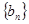 前n项和
前n项和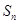
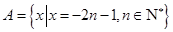 ,
,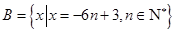 ,设
,设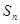 是等差数列
是等差数列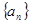 的前
的前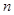 项和,若
项和,若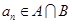 ,且首项
,且首项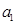 是
是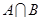 中的最大数,
中的最大数, 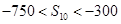 .
.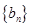 满足
满足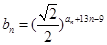 ,求
,求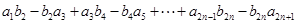 的值.
的值. 的前
的前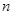 项和
项和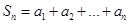 ,若
,若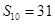 ,
,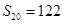 ,则
,则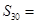 ( )
( )