题目内容
13.已知平面内的向量$\overrightarrow{OA},\overrightarrow{OB}$满足:|$\overrightarrow{OA}$|=1,($\overrightarrow{OA}$+$\overrightarrow{OB}$)•($\overrightarrow{OA}$-$\overrightarrow{OB}$)=0,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°,又$\overrightarrow{OP}$=λ${\;}_{1}\overrightarrow{OA}$+λ${\;}_{2}\overrightarrow{OB}$,0≤λ1≤1,1≤λ2≤2,则由满足条件的点P所组成的图形的面积是( )| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
分析 根据条件建立平面直角坐标系,将满足不等式表示的可行域表示出来,从而将P点对应的图形描述出来,即可求解.
解答 解:∵|$\overrightarrow{OA}$|=1,($\overrightarrow{OA}$+$\overrightarrow{OB}$)•($\overrightarrow{OA}$-$\overrightarrow{OB}$)=0,得到${\overrightarrow{OA}}^{2}={\overrightarrow{OB}}^{2}$,即OA=OB,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°,
三角形AOB是等边三角形,则不妨以O为原点,以OA方向为x轴正方向,建立坐标系,如图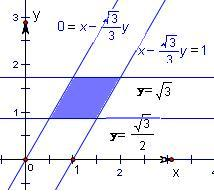
则 $\overrightarrow{OA}$=(1,0),$\overrightarrow{OB}=(\frac{1}{2},\frac{\sqrt{3}}{2})$
又 $\overrightarrow{OP}$=λ${\;}_{1}\overrightarrow{OA}$+λ${\;}_{2}\overrightarrow{OB}$,0≤λ1≤1,1≤λ2≤2,
令 $\overrightarrow{OP}$=(x,y),则 $\overrightarrow{OP}$=(λ1$+\frac{1}{2}$λ2,$\frac{\sqrt{3}}{2}$λ2)
∴$\left\{\begin{array}{l}{x={λ}_{1}+\frac{1}{2}{λ}_{2}}\\{y=\frac{\sqrt{3}}{2}{λ}_{2}}\end{array}\right.$,∴$\left\{\begin{array}{l}{{λ}_{1}=x-\frac{\sqrt{3}}{3}y}\\{{λ}_{2}=\frac{2\sqrt{3}}{3}y}\end{array}\right.$,
由于0≤λ1≤1,1≤λ2≤2,
∴$\left\{\begin{array}{l}{0≤x-\frac{\sqrt{3}}{3}y≤1}\\{1≤\frac{2\sqrt{3}}{3}y≤2}\end{array}\right.$
其表示的平面区域如图示:
由图可知阴影部分的面积为$\frac{\sqrt{3}}{2}×1$=$\frac{\sqrt{3}}{2}$.
故选D.
点评 本题主要考查平面区域的面积问题,是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合有关面积公式求解.

 阅读快车系列答案
阅读快车系列答案| A. | 不能作出满足要求的三角形 | B. | 作出一个钝角三角形 | ||
| C. | 作出一个直角三角形 | D. | 作出一个锐角三角形 |
| A. | y=cosx | B. | y=lg|x| | C. | y=-x2+1 | D. | y=x3 |
| A. | 周期为π的偶函数 | B. | 周期为$\frac{π}{2}$的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为π的奇函数 |
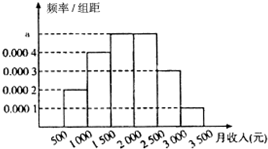 统计局就某地居民的月收入情况调查了10000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在[500,1000).
统计局就某地居民的月收入情况调查了10000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在[500,1000).