题目内容
4．
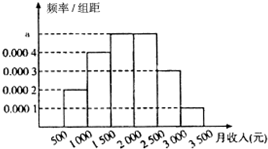统计局就某地居民的月收入情况调查了10000人，并根据所得数据画了样本频率分布直方图，每个分组包括左端点，不包含右端点，如第一组表示收入在[500，1000）．（1）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这10000人中用分层抽样方法抽出100人作进一步分析，则月收入在[1500，2500）的应抽取多少人？
（2）根据频率分布直方图估计样本数据的平均数．
分析 （1）利用频率直方图的数据求解a=$\frac{0.5}{1000}$，得出月收入在[1500，2500）的频率为0.5，所以抽出100人中月收入在[1500，2500）的人数为0.5×100
（2）利用矩形的中间数据与频率乘积的和得出平均值即可．
解答 解：（1）因为（0.0002+0.0004+0.0003+0.0001）×500=0.5，所以a=$\frac{0.5}{1000}$=0.0005，
月收入在[1500，2500）的频率为0.5，
所以月收入在[1500，2500）的人数为0.5×100=50人．
（2）∵（750×0.0002+1250×0.0004+1750×0.0005+2250×0.0005+2750×0.0003+3250×0.0001）×500=1900（元）
∴频率分布直方图估计样本数据的平均数1900
点评 本题考察了频率直方图的运用，解决统计分析问题，属于中档题，计算较麻烦．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
14．数列{an}中，a1=1，a2=3，an+2是anan+1的个位数字，Sn是{an}的前n项和，则S2015=（ ）
| A． | 8733 | B． | 8710 | C． | 8726 | D． | 8717 |
15．已知复数z=$\frac{1+i}{1-i}$，则|z|=（ ）
| A． | 2 | B． | 1 | C． | 0 | D． | $\sqrt{2}$ |
12．
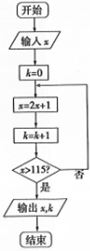如图所示的程序框图中，若输入x的值为10，则输出的x与k的值的和为（ ）
如图所示的程序框图中，若输入x的值为10，则输出的x与k的值的和为（ ）| A． | 179 | B． | 173 | C． | 90 | D． | 84 |
9．若函数f（x）=x-$\frac{2}{x}$-3lnx+k在其定义域上有三个零点，则实数k的取值范围是（ ）
| A． | （-∞，1-3ln2） | B． | （1，3ln2-1） | C． | （1-3ln2，1） | D． | （1，+∞） |
13．已知平面内的向量$\overrightarrow{OA}，\overrightarrow{OB}$满足：|$\overrightarrow{OA}$|=1，（$\overrightarrow{OA}$+$\overrightarrow{OB}$）•（$\overrightarrow{OA}$-$\overrightarrow{OB}$）=0，且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°，又$\overrightarrow{OP}$=λ${\;}_{1}\overrightarrow{OA}$+λ${\;}_{2}\overrightarrow{OB}$，0≤λ1≤1，1≤λ2≤2，则由满足条件的点P所组成的图形的面积是（ ）
| A． | 2 | B． | $\sqrt{3}$ | C． | 1 | D． | $\frac{\sqrt{3}}{2}$ |