题目内容
3.函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈(-1,1]时,f(x)=1-x2,函数g(x)=$\left\{\begin{array}{l}{lg|x|,x≠0}\\{1,x=0}\end{array}\right.$则函数h(x)=f(x)-g(x)在区间[-5,10]内零点的个数为( )| A. | 8 | B. | 12 | C. | 13 | D. | 14 |
分析 函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈(-1,1]时f(x)=1-x2,故其为周期性函数,函数g(x)是一个偶函数,作出它们的图象,由图象上看交点个数.对边界处的关键点要作准.
解答 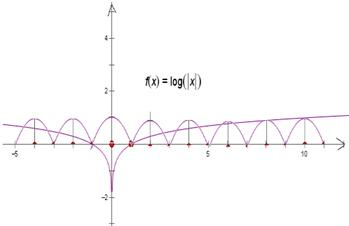 解:作出区间[-5,10]上的两个函数的图象,
解:作出区间[-5,10]上的两个函数的图象,
y轴右边最后一个公共点是(10,1)y轴左边有四个交点,
y轴右边是9个交点,y轴上有一个交点,总共是14个交点.
故选:D.
点评 考查答题者使用图象辅助作题的意识与能力,本题是一道中档题.

练习册系列答案
相关题目
13.已知平面内的向量$\overrightarrow{OA},\overrightarrow{OB}$满足:|$\overrightarrow{OA}$|=1,($\overrightarrow{OA}$+$\overrightarrow{OB}$)•($\overrightarrow{OA}$-$\overrightarrow{OB}$)=0,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°,又$\overrightarrow{OP}$=λ${\;}_{1}\overrightarrow{OA}$+λ${\;}_{2}\overrightarrow{OB}$,0≤λ1≤1,1≤λ2≤2,则由满足条件的点P所组成的图形的面积是( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
11.已知某组数据采用了四种不同的回归方程进行回归分析,则回归效果最好的相关指数R2的值是( )
| A. | 0.97 | B. | 0.83 | C. | 0.32 | D. | 0.17 |
8.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,且$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=$\frac{1}{2}$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
12.数列1,$\frac{1}{2}$,$\frac{2}{1},\frac{1}{3},\frac{2}{2},\frac{3}{1},\frac{1}{4},\frac{2}{3},\frac{3}{2},\frac{4}{1},…$中第50个数是( )
| A. | $\frac{7}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |