题目内容

1．某人要作一个三角形，要求它的三条高的长度分别是$\frac{1}{13}$，$\frac{1}{11}$，$\frac{1}{5}$，则此人将（　　）
A．不能作出满足要求的三角形B．作出一个钝角三角形
C．作出一个直角三角形D．作出一个锐角三角形

分析 先设出三边来，根据面积相等和三条高的长度求得a，b和c的比，进而利用余弦定理求得cosA通过结果小于0判断出A为钝角．

解答 解：设三边分别为a，b，c，利用面积相等可知$\frac{1}{13}$a=$\frac{1}{11}$b=$\frac{1}{5}$c，
∴a：b：c=13：11：5
令a=13，b=11，c=5
由余弦定理得cosA=$\frac{{5}^{2}+1{1}^{2}-1{3}^{2}}{2×5×11}$＜0，所以角A为钝角，
故选：B．

点评 本题主要考查了余弦定理的应用和三角形形状的判断．在判断三角形的形状时常可通过判断三个角的余弦值正负来判断三角形是否是钝角三角形．

练习册系列答案
相关题目
11．已知函数f（x）=Asin（$\frac{π}{3}x$+φ），（A＞0，0＜φ＜$\frac{π}{2}$），y=f（x）的部分图象如图所示，P，Q分别为该图象上相邻的最高点和最低点，点P在x轴上的射影为R（1，0），cos∠PRQ=-$\frac{4}{5}$．
（1）求A，φ的值；
（2）将函数f（x）的图象上所有点向右平移θ（θ＞0）个单位，得到函数g（x）的图象，若g（x）在区间[0，3]上单调递增，求θ的最小值．
12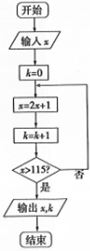．如图所示的程序框图中，若输入x的值为10，则输出的x与k的值的和为（　　）
A．179B．173C．90D．84
9．若函数f（x）=x-$\frac{2}{x}$-3lnx+k在其定义域上有三个零点，则实数k的取值范围是（　　）
A．（-∞，1-3ln2）B．（1，3ln2-1）C．（1-3ln2，1）D．（1，+∞）
16．已知数列{an}满足an+1=3an+4，（n∈N*）且a1=1，
（Ⅰ）求证：数列{an+2}是等比数列；
（Ⅱ）求数列{an}的前n项和Sn．
6．已知f（α）=$\frac{{cos（{3π+α}）cos（{\frac{3π}{2}+α}）sin（{-α}）}}{{tan（{-π-α}）sin（{3π-α}）cos（{-π-α}）}}$．
（1）化简f（α）；
（2）已知角α为锐角，$f（{α+\frac{π}{6}}）=\frac{3}{5}$，求f（α）的值．
13．已知平面内的向量$\overrightarrow{OA}，\overrightarrow{OB}$满足：|$\overrightarrow{OA}$|=1，（$\overrightarrow{OA}$+$\overrightarrow{OB}$）•（$\overrightarrow{OA}$-$\overrightarrow{OB}$）=0，且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°，又$\overrightarrow{OP}$=λ${\;}_{1}\overrightarrow{OA}$+λ${\;}_{2}\overrightarrow{OB}$，0≤λ1≤1，1≤λ2≤2，则由满足条件的点P所组成的图形的面积是（　　）
A．2B．$\sqrt{3}$C．1D．$\frac{\sqrt{3}}{2}$
10．已知圆D的半径为1，圆C的方程是（x-2）2+（y+1）2=4，若圆D与圆C相切于点（4，-1），则圆D的标准方程是（x-5）2+（y+1）2=1 或（x-3）2+（y+1）2=1．
11．已知某组数据采用了四种不同的回归方程进行回归分析，则回归效果最好的相关指数R2的值是（　　）
A．0.97B．0.83C．0.32D．0.17

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网