题目内容
1．已知f（x）是定义在（0，+∞）的函数．对任意两个不相等的正数x1，x2，都有$\frac{{x}_{2}f（{x}_{1}）-{x}_{1}f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0，记a=$\frac{f（{3}^{0.2}）}{{3}^{0.2}}$，b=$\frac{f（0．{3}^{2}）}{0．{3}^{2}}$，c=$\frac{f（lo{g}_{2}5）}{lo{g}_{2}5}$，则（ ）| A． | a＜b＜c | B． | b＜a＜c | C． | c＜a＜b | D． | c＜b＜a |
分析 由题意可得函数$\frac{f（x）}{x}$是（0，+∞）上的增函数，比较大小可得0.32＜30.2＜log25，故可得答案．
解答 解：∵f（x）是定义在（0，+∞）上的函数，对任意两个不相等的正数x1，x2，都有$\frac{{x}_{2}f（{x}_{1}）-{x}_{1}f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0，
∴函数$\frac{f（x）}{x}$是（0，+∞）上的增函数，
∵1＜30.2＜3，0＜0.32＜1，log25＞2，
∴0.32＜30.2＜log25，
∴b＜a＜c．
故选：B．
点评 本题主要考查利用函数的单调性比较大小，考查学生对指数函数、对数函数性质的运用能力，属于中档题．
练习册系列答案
相关题目
11．
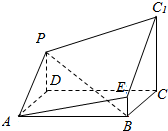如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的，其中AB=4，BC=2，CC1=3，BE=1，则点F到平面AEC的距离为（ ）
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的，其中AB=4，BC=2，CC1=3，BE=1，则点F到平面AEC的距离为（ ）| A． | $\frac{1}{7}$ | B． | $\frac{\sqrt{21}}{7}$ | C． | $\frac{4\sqrt{21}}{7}$ | D． | $\frac{8}{7}$ |
12．对函数f（x）=$\sqrt{3}sinxcosx+{cos}^{2}x-\frac{1}{2}$的表述错误的是（ ）
| A． | 最小正周期为π | |
| B． | 函数y=sin2x向左平移$\frac{π}{12}$个单位可得到f（x） | |
| C． | f（x）在区间$（-\frac{π}{3}，\frac{π}{6}）$上递增 | |
| D． | 点$（\frac{π}{6}，0）$是f（x）的一个对称中心 |
6．对定义在R上的函数f（x），若实数x0满足f（x0）=x0，则x0称为f（x）的一个不动点．设二次函数f（x）=x2+mx-m+2，若f（x）在[0，+∞）上有不动点，则m的取值范围是（ ）
| A． | [-1-2$\sqrt{2}$，2] | B． | （-∞，-1-2$\sqrt{2}$]∪[2，+∞） | C． | [-1，2] | D． | （-∞，-1]∪[2，+∞） |
13．定义在R上的偶函数f（x）满足：对任意的x1，x2∈[0，+∞）（x1≠x2），有（x2-x1）[f（x2）-f（x1）]＜0．则（ ）
| A． | f（1）＜f（-2）＜f（3） | B． | f（3）＜f（1）＜f（-2） | C． | f（一2）＜f（1）＜f（3） | D． | f（3）＜f（-2）＜f（1） |
10．直角坐标系中，方程|x|•y=1表示的曲线是（ ）
| A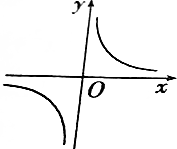． |  | B． |  | ||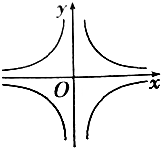
| C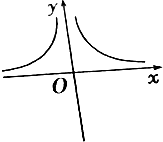． |  | D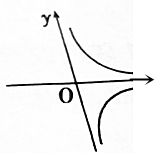． |  |