题目内容
11．
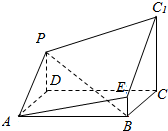如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的，其中AB=4，BC=2，CC1=3，BE=1，则点F到平面AEC的距离为（ ）| A． | $\frac{1}{7}$ | B． | $\frac{\sqrt{21}}{7}$ | C． | $\frac{4\sqrt{21}}{7}$ | D． | $\frac{8}{7}$ |
分析 建立如图所示的坐标系，则F（0，0，2），A（2，0，0），E（2，4，1），C（0，4，0），求出平面AEC的法向量，$\overrightarrow{AF}$=（-2，0，2），即可求出点F到平面AEC的距离．
解答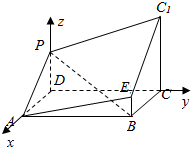 
解：建立如图所示的坐标系，则F（0，0，2），A（2，0，0），E（2，4，1），C（0，4，0），
设平面AEC的法向量为$\overrightarrow{n}$=（x，y，z），则
∵$\overrightarrow{AE}$=（0，4，1），$\overrightarrow{AC}$=（-2，4，0），
∴$\left\{\begin{array}{l}{4y+z=0}\\{-2x+4y=0}\end{array}\right.$，
∴取$\overrightarrow{n}$=（2，1，-4），
∵$\overrightarrow{AF}$=（-2，0，2），
∴点F到平面AEC的距离为$\frac{|-4-8|}{\sqrt{4+1+16}}$=$\frac{4\sqrt{21}}{7}$．
故选：C．
点评 本题考查求点F到平面AEC的距离，考查向量方法的运用，正确求出平面的法向量是关键．
练习册系列答案
相关题目
1．过点A（-2，3）作直线与抛物线y2=8x在第一象限相切于点B，记抛物线的焦点为F，则直线BF的斜率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
2．P是△ABC内一点．△ABC，△ABP．△ACP的面积分别对应记为S，S1，S2．已知$\overrightarrow{CP}$=$\frac{3λ}{4}$$\overrightarrow{CA}$+$\frac{λ}{4}$$\overrightarrow{CB}$，其中λ∈（0，1）．若$\frac{S}{{S}_{1}}$=3则$\frac{{S}_{2}}{{S}_{1}}$=（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
19．设集合A={x|-1＜x＜4}，B={-1，1，2，4}，则A∩B=（ ）
| A． | {1，2} | B． | {-1，4} | C． | {-1，2} | D． | {2，4} |
6．函数f（x）=ax（a＞0且a≠1）在区间[1，2]上的最大值比最小值大$\frac{a}{4}$，则实数a的值为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{4}或\frac{5}{4}$ | D． | $\frac{3}{4}或\frac{5}{4}$ |
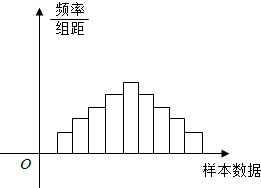在样本的频率分布直方图中，共有9个小长方形，若第一个长方形的面积为0.04，前五个与后五个长方形的面积分别成等差数列且公差是互为相反数，若样本容量为800，则中间一组（即第五组）的频数为160．