题目内容
12.在数列{an}中,a1=1,a2=m(m≠-1),前n项和Sn满足$\frac{1}{S_n}=\frac{1}{a_n}-\frac{1}{{{a_{n+1}}}}(n≥2)$.(1)求a3(用m表示);
(2)求证:数列{Sn}是等比数列;
(3)若m=1,现按如下方法构造项数为2k的有穷数列{bn}:当n=1,2,…,k时,bn=a2k-n+1;当n=k+1,k+2,…,2k时,bn=anan+1,记数列{bn}的前n项和Tn,试问:$\frac{{{T_{2k}}}}{T_k}$是否能取整数?若能,请求出k的取值集合;若不能,请说明理由.
分析 (1)利用递推关系式,令n=2,通过a1=1,a2=m,求出a3即可.
(2)递推关系式转化为:$\frac{1}{S_n}=\frac{1}{{{S_n}-{S_{n-1}}}}-\frac{1}{{{S_{n+1}}-{S_n}}}$,化简推出数列{Sn}是等比数列.
(3)由m=1,求出S1=1,S2=2,求出${S_n}={2^{n-1}}$,得到通项公式,然后求解$\frac{{{T_{2k}}}}{T_k}$的分母与分子,讨论要使$\frac{{{T_{2k}}}}{T_k}$取整数,需$\frac{{{2^k}+1}}{3}$为整数,推出k的取值集合为{k|k=2n-1,n∈Z*}时,$\frac{{{T_{2k}}}}{T_k}$取整数.
解答 解:(1)令n=2,则$\frac{1}{S_2}=\frac{1}{a_2}-\frac{1}{a_3}$,将a1=1,a2=m代入,有$\frac{1}{1+m}=\frac{1}{m}-\frac{1}{a_3}$,
解得${a_3}={m^2}+m$…(5分)
(2)由$\frac{1}{S_n}=\frac{1}{a_n}-\frac{1}{{{a_{n+1}}}}(n≥2)$,得$\frac{1}{S_n}=\frac{1}{{{S_n}-{S_{n-1}}}}-\frac{1}{{{S_{n+1}}-{S_n}}}$,化简得${S_n}^2={S_{n-1}}{S_{n+1}}$,
又Sn≠0,∴数列{Sn}是等比数列…(10分)
(3)由m=1,∴S1=1,S2=2,又数列{Sn}是等比数列,∴${S_n}={2^{n-1}}$,
∴${a_n}={S_n}-{S_{n-1}}={2^{n-1}}-{2^{n-2}}={2^{n-2}}(n≥2)$,
当n=1,2,…,k时,bn依次为a2k,a2k-1,…,ak+1,
∴${T_k}={S_{2k}}-{S_k}={2^{2k-1}}-{2^{k-1}}={2^{k-1}}({2^k}-1)$…(13分)
当n=k+1,k+2,…,2k,${b_n}={a_n}{a_{n+1}}={2^{2n-3}}$,∴${T_{2k}}-{T_k}={2^{2(k+1)-3}}•\frac{{1-{4^k}}}{1-4}=\frac{{{2^{2k-1}}({4^k}-1)}}{3}$,
∴$\frac{{{T_{2k}}}}{T_k}=\frac{{{T_{2k}}-{T_k}}}{T_k}+1=\frac{{{2^k}({2^k}+1)}}{3}+1$,要使$\frac{{{T_{2k}}}}{T_k}$取整数,需$\frac{{{2^k}+1}}{3}$为整数,
令${c_k}=\frac{{{2^k}+1}}{3}$,
∴${c_{k+2}}-{c_k}=\frac{{{2^{k+2}}+1}}{3}-\frac{{{2^k}+1}}{3}={2^k}$,
∴ck+2,ck要么都为整数,要么都不是整数,
又c1=1,${c_2}=\frac{5}{3}$,
∴当且仅当k为奇数时,ck为整数,
即k的取值集合为{k|k=2n-1,n∈Z*}时,$\frac{{{T_{2k}}}}{T_k}$取整数.…(16分)
点评 本题考查数列的综合应用,数列的递推关系式以及数列求和,考查分类讨论思想的应用,考查计算能力.

 优加精卷系列答案
优加精卷系列答案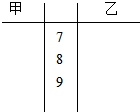 某班级从甲乙两位同学选派一人参加数学竞赛,老师对他们平时的10次模拟测试成绩(单位:分)进行了记录如下:
某班级从甲乙两位同学选派一人参加数学竞赛,老师对他们平时的10次模拟测试成绩(单位:分)进行了记录如下:| 甲 | 79 | 83 | 96 | 89 | 86 | 78 | 85 | 95 | 82 | 87 |
| 乙 | 81 | 95 | 83 | 76 | 91 | 86 | 96 | 77 | 82 | 93 |
(2)分别计算这两组数据的平均数和方差,并根据你的计算结果,判断选派哪位学生参加合适?
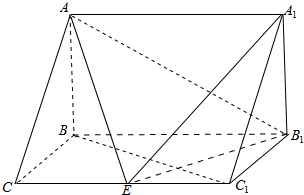 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=$\frac{π}{3}$.