题目内容
20.已知$\frac{2+3i}{m-3i}$为实数,其中i是虚数单位,则实数m的值为-2.分析 化简复数为a+bi的形式,然后利用复数的概念,求解即可.
解答 解:$\frac{2+3i}{m-3i}$=$\frac{(2+3i)(m+3i)}{(m-3i)(m+3i)}$=$\frac{2m-9+(3m+6)i}{{m}^{2}+9}$,
已知$\frac{2+3i}{m-3i}$为实数,
可得3m+6=0,解得m=-2.
故答案为:-2.
点评 本题考查复数的除法的运算法则的应用,复数的基本概念的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若集合A={x|x>-1},B={x|-2<x<3},则A∩B=( )
| A. | {x|x>-1} | B. | {x|-1<x<3} | C. | {x|x>-2} | D. | {x|-2<x<3} |
9.设O为坐标原点,直线l经过点P(1,1)且与OP垂直,则直线l的方程为( )
| A. | x+y+2=0 | B. | x+y-1=0 | C. | x+y=0 | D. | x+y-2=0 |
10.函数f(x)=x•sin($\frac{3π}{2}$+x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
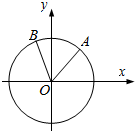 如图,在平面直角坐标系xOy中,以Ox轴为始边作角α和β,$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,其终边分别交单位圆于A,B两点.若A,B两点的横坐标分别是$\frac{3}{5}$,-$\frac{{\sqrt{2}}}{10}$. 试求
如图,在平面直角坐标系xOy中,以Ox轴为始边作角α和β,$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,其终边分别交单位圆于A,B两点.若A,B两点的横坐标分别是$\frac{3}{5}$,-$\frac{{\sqrt{2}}}{10}$. 试求