题目内容
2.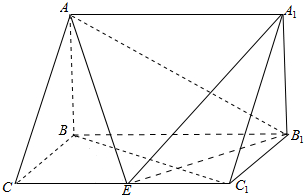 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=√2,∠BCC1=π3.
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=√2,∠BCC1=π3.(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)试在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1;
(Ⅲ)在(Ⅱ)的条件下,求二面角A-EB1-A1的正切值.
分析 (Ⅰ)由余弦定理即可求出C1B=√3,从而可说明C1B⊥BC,而由AB⊥平面BB1C1C可得到EB1⊥AB,从而根据线面垂直的判定定理即可得到C1B⊥平面ABC;
(Ⅱ)连接BE,由上面知EB1⊥BE,设CE=x,(0<x<2),分别根据余弦定理可得到BE2,EB12,从而根据BE2+EB12=BB12即可求出x=1,从而E点的位置为棱CC1的中点;
(Ⅲ)容易说明∠BAE等于二面角A-EB1-A1平面角的大小,并且△ABE是直角三角形,BE=1,AB=√2,从而便能求出二面角A-EB1-A1的正切值.
解答 解:(Ⅰ)证明:△BCC1中,BC=1,CC1=BB1=2,∠BCC1=π3;
∴由余弦定理:BC12=1+4−2=3;
∴BC1=√3;
∴BC2+BC12=CC12;
∴C1B⊥BC;
又AB⊥平面BB1C1C,C1B?平面BB1C1C;
∴C1B⊥AB,AB∩BC=B;
∴C1B⊥平面ABC;
(Ⅱ)如图,连接BE,AB⊥平面BB1C1C;
∴EB1⊥AB;
若EA⊥EB1,即EB1⊥EA,AB∩EA=A;
∴EB1⊥平面ABE,BE?平面ABE;
∴EB1⊥BE;
设CE=x.则EC1=2-x;
在△BCE中,由余弦定理得BE2=x2-x+1;
∠B1C1E=2π3,∴在△EB1C1中,由余弦定理得EB12=1+(2-x)2+(2-x)=x2-5x+7;
在Rt△BB1E中,BE2+EB12=BB12;
∴2x2-6x+8=4;
解得x=1,或x=2(舍去);
∴E为CC1中点时,EA⊥EB1;
(Ⅲ)由前面知AB⊥EB1,AE⊥EB1;
∴∠BAE等于二面角A-EB1-A1的大小;
AB⊥BB1C1C,∴AB⊥BE;
∴在Rt△ABE中BE=1,AB=√2,tan∠BAE=1√2=√22;
∴二面角A-EB1-A1的正切值为√22.
点评 考查余弦定理,直角三角形边的关系,线面垂直的性质,线面垂直的判定定理,以及二面角平面角的概念及求法,正切函数的定义.

(参考值:P(μ-σ<X≤μ+σ)=0.6826;P(μ-2σ<X≤μ+2σ)=0.9544;P(μ-3σ<X≤μ+3σ)=0.9974)
| A. | 0.4772 | B. | 0.1574 | C. | 0.2718 | D. | 0.1359 |
| A. | {x|-1≤x<0或x≥2} | B. | {x|-1≤x≤0或x≥2} | C. | {x|-1≤x≤0或x>2} | D. | {x|0≤x<2} |
| A. | {x|x>-1} | B. | {x|-1<x<3} | C. | {x|x>-2} | D. | {x|-2<x<3} |
 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40