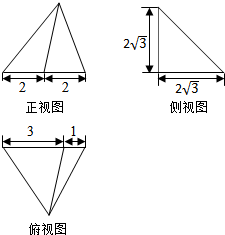
题目内容
13.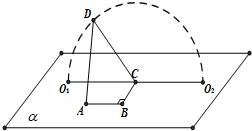 如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
分析 由已知得到BC⊥平面O1DCO2,以C为原点,CB为x轴,CO2为y轴,过C作平面ABC的直线为z轴,建立空间直角坐标系,利用向量法能推导出当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值一直减小.
解答 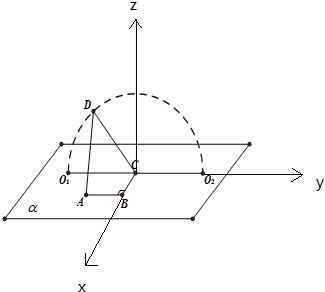 解:∵A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC,
解:∵A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC,
∴BC⊥平面O1DCO2,
以C为原点,CB为x轴,CO2为y轴,过C作平面ABC的直线为z轴,建立空间直角坐标系,
则A(1,-1,0),B(1,0,0),C(0,0,0),D(0,y,z),其中-$\sqrt{3}≤y≤\sqrt{3}$,0$≤z≤\sqrt{3}$,
∴$\overrightarrow{AD}$=(-1,y+1,z),$\overrightarrow{BC}$=(-1,0,0),
∴cos<$\overrightarrow{AD},\overrightarrow{BC}$>=$\frac{1}{\sqrt{1+(y+1)^{2}+{z}^{2}}}$,
∵当点D从O1顺时针转动到O2的过程中,
y+1的取值从1$-\sqrt{3}$到1+$\sqrt{3}$逐渐增大,z的值先0逐渐增加到$\sqrt{3}$,再从$\sqrt{3}$逐渐减少到0,
∴异面直线AD与BC所成角的余弦值一直减小.
故选:A.
点评 本题考查异面直线所成角的余弦值的求法及应用,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知b2-4ac是一元二次方程ax2+bx+c=0(a≠0)的一个实数根,则( )
| A. | ab≤$\frac{1}{8}$ | B. | ab≥$\frac{1}{8}$ | C. | ab$≥\frac{1}{4}$ | D. | ab$≤\frac{1}{4}$ |
18.已知函数f(x)=lg(x2-2ax+2),若对任意的x1,x2∈(-∞,1]且x1≠x2,均有[f(x1)-f(x2)]( x1-x2 )<0成立,则实数a的取值范围是( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (1,$\frac{3}{2}$) | D. | [1,$\frac{3}{2}$] |
 如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.
如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.