题目内容
4.化简:$\frac{2co{s}^{4}x-2co{s}^{2}x+\frac{1}{2}}{2tan(\frac{π}{4}-x)si{n}^{2}(\frac{π}{4}+x)}$.分析 由诱导公式可得sin($\frac{π}{4}$+x)=cos($\frac{π}{4}$-x),整体代入要求的式子结合三角函数公式化简可得.
解答 解:由诱导公式可得sin($\frac{π}{4}$+x)=sin[$\frac{π}{2}$-($\frac{π}{4}$-x)]=cos($\frac{π}{4}$-x),
∴$\frac{2co{s}^{4}x-2co{s}^{2}x+\frac{1}{2}}{2tan(\frac{π}{4}-x)si{n}^{2}(\frac{π}{4}+x)}$=$\frac{\frac{1}{2}(4co{s}^{4}x-4co{s}^{2}x+1)}{2•\frac{sin(\frac{π}{4}-x)}{cos(\frac{π}{4}-x)}•co{s}^{2}(\frac{π}{4}-x)}$
=$\frac{\frac{1}{2}(2co{s}^{2}x-1)^{2}}{2sin(\frac{π}{4}-x)cos(\frac{π}{4}-x)}$=$\frac{\frac{1}{2}(cos2x)^{2}}{sin(\frac{π}{2}-2x)}$=$\frac{\frac{1}{2}(cos2x)^{2}}{cos2x}$=$\frac{1}{2}$cos2x.
点评 本题考查三角函数的化简求值,涉及诱导公式和二倍角公式以及整体思想,属中档题.

练习册系列答案
相关题目
15.设A(-2,3),B(3,3),若直线ax+y+2=0与线段AB有交点,则实数a的取值范围是( )
| A. | [-$\frac{5}{3}$,$\frac{5}{2}$] | B. | (-∞,-$\frac{5}{3}$]∪[$\frac{5}{2}$,+∞) | C. | (-∞,-$\frac{5}{2}$]∪[$\frac{5}{3}$,+∞) | D. | [-$\frac{5}{2}$,$\frac{5}{3}$] |
12.函数y=log${\;}_{\frac{1}{2}}$(1-2x)的值域为( )
| A. | (-∞,+∞) | B. | (-∞,0) | C. | (0,+∞) | D. | (1,+∞) |
16.图是截去了一个角的正方体,则它的俯视图为( )
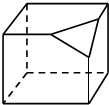

| A. | 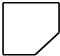 | B. | 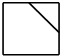 | C. | 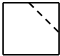 | D. | 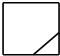 |
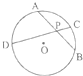
13.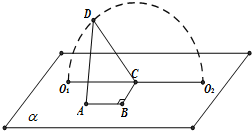 如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
 如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
14.下面程序的功能是( )
INPUT“n=“;n
A=1
i=1
WHILE i<=n
A=A*i
i=i+1
WEND
PRINT A
END.
INPUT“n=“;n
A=1
i=1
WHILE i<=n
A=A*i
i=i+1
WEND
PRINT A
END.
| A. | 计算1+2+…+n | B. | 计算1+(1+2)+(1+2+3)+…(1+2+3+…+n) | ||
| C. | 计算n! | D. | 以上都不对 |