题目内容
7.已知等差数列{an}的公差为d(d≠0),等比数列{bn}的公比为q(q>0),且满足a1=b1=1,a2=b3,a6=b5.(1)求数列{an}的通项公式;(2)证明:对一切n∈N*,令bn=an•an+1,都有$\frac{1}{4}$≤$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$<$\frac{1}{3}$.
分析 (1)利用等差、等比数列的定义计算即得结论;
(2)通过分离分母可得$\frac{1}{{b}_{n}}$=$\frac{1}{3}$($\frac{1}{3n-2}$-$\frac{1}{3n+1}$),并项相加可得$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$=$\frac{1}{3}$(1-$\frac{1}{3n+1}$),进而可得结论.
解答 (1)解:由题得:$\left\{\begin{array}{l}{{a}_{2}={b}_{3}}\\{{a}_{6}={b}_{5}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{1+d={q}^{2}}\\{1+5d={q}^{4}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{d=3}\\{q=2}\end{array}\right.$,
故an=3n-2;
(2)证明:∵$\frac{1}{{b}_{n}}$=$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{(3n-2)(3n+1)}$=$\frac{1}{3}$($\frac{1}{3n-2}$-$\frac{1}{3n+1}$),
∴$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$=$\frac{1}{3}$(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+…+$\frac{1}{3n-2}$-$\frac{1}{3n+1}$)=$\frac{1}{3}$(1-$\frac{1}{3n+1}$),
∵当n∈N*时,$\frac{1}{{b}_{n}}$>0,
∴n=1时,$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$≥$\frac{1}{{b}_{1}}$=$\frac{1}{4}$,
又∵1-$\frac{1}{3n+1}$是单调递增的,
∴$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$=$\frac{1}{3}$(1-$\frac{1}{3n+1}$)<$\frac{1}{3}$,
故对一切n∈N*,都有:$\frac{1}{4}$≤$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$<$\frac{1}{3}$.
点评 本题考查求数列的通项和前n项和的取值范围,注意解题方法的积累,属于中档题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案女士消费情况:
| 消费金额 | (0.200) | [200,400) | [400.600) | [600,800) | [800,1000] |
| 人数 | 10 | 25 | 35 | 30 | X |
| 消费金额 | (0.200) | [200,400) | [400.600) | [600,800) | [800.1000] |
| 人数 | 15 | 30 | 25 | Y | 5 |
(2)若消费金额不低于600元的网购者为“网购达人,低于600元的网购者为“非网购达人”根据以上统计数据填写答题卡中的2×2列联表,并冋答能否在犯错误的概率不超过0.05的前提下认为“是否为网购达人与性别有关?”
附表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,则A=2,ω=2,F($\frac{π}{3}$)=1.
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,则A=2,ω=2,F($\frac{π}{3}$)=1.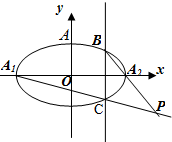 如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.
如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.