题目内容
14.f(x)=$\left\{\begin{array}{l}{x^2}-4x+3,x≥0\\ \frac{x+3}{1-2x},x<0\end{array}$(1)作出函数的大致图象;
(2)求不等式f(x)>f(1)的解集.
分析 (1)分类讨论化简函数的解析式,从而画出函数的图象.
(2)结合函数f(x)的图象可得f(-3)=f(1)=f(3)=0,数形结合可得不等式f(x)>f(1)的解集.
解答  解:(1)对于函数f(x)=$\left\{\begin{array}{l}{x^2}-4x+3,x≥0\\ \frac{x+3}{1-2x},x<0\end{array}$,当x≥0时,f(x)=(x-3)(x-1);
解:(1)对于函数f(x)=$\left\{\begin{array}{l}{x^2}-4x+3,x≥0\\ \frac{x+3}{1-2x},x<0\end{array}$,当x≥0时,f(x)=(x-3)(x-1);
当 x<0时,f(x)=-$\frac{x+3}{2x-1}$=-($\frac{x-\frac{1}{2}+\frac{7}{2}}{2(x-\frac{1}{2})}$)=-($\frac{1}{2}$+$\frac{7}{4(x-\frac{1}{2})}$)=-$\frac{1}{2}$-$\frac{7}{4x-2}$,
故函数f(x)的图象如图所示.
(2)结合函数f(x)的图象可得f(-3)=f(1)=f(3)=0,
数形结合可得不等式f(x)>f(1)的解集为{x|-3<x<1,或x>3}.
点评 本题主要考查分段函数的应用,分式不等式的解法,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
4.a=${∫}_{0}^{2}$xdx,b=${∫}_{0}^{2}$exdx,c=${∫}_{0}^{2}$sinxdx,则a、b、c大小关系是( )
| A. | a<c<b | B. | a<b<c | C. | c<b<a | D. | c<a<b |
2.定义在R上的函数f(x)满足$f(x)=\left\{{\begin{array}{l}{{{log}_3}(9-x),x≤0}\\{f(x-1),x>0}\end{array}}\right.$,则f(3)的值为( )
| A. | 1 | B. | 2 | C. | -2 | D. | -3 |
6.在△ABC中,a=4,b=5,c=6,则$\frac{sin2A}{sinC}$=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.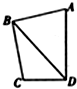 已知一颗小米粒等可能地落入如图所示的平面四边形 ABCD(AD=$\frac{3}{2}$CD)内的任意一个位置,如果通过大量的试验发现米粒落入△BCD内的频率稳定在$\frac{2}{5}$附近,记点 B到直线 AD的距离与点 B到直线CD的距离的比值为λ,则函数f(x)=cos2x+2λsinx的最大值与最小值之和为( )
已知一颗小米粒等可能地落入如图所示的平面四边形 ABCD(AD=$\frac{3}{2}$CD)内的任意一个位置,如果通过大量的试验发现米粒落入△BCD内的频率稳定在$\frac{2}{5}$附近,记点 B到直线 AD的距离与点 B到直线CD的距离的比值为λ,则函数f(x)=cos2x+2λsinx的最大值与最小值之和为( )
 已知一颗小米粒等可能地落入如图所示的平面四边形 ABCD(AD=$\frac{3}{2}$CD)内的任意一个位置,如果通过大量的试验发现米粒落入△BCD内的频率稳定在$\frac{2}{5}$附近,记点 B到直线 AD的距离与点 B到直线CD的距离的比值为λ,则函数f(x)=cos2x+2λsinx的最大值与最小值之和为( )
已知一颗小米粒等可能地落入如图所示的平面四边形 ABCD(AD=$\frac{3}{2}$CD)内的任意一个位置,如果通过大量的试验发现米粒落入△BCD内的频率稳定在$\frac{2}{5}$附近,记点 B到直线 AD的距离与点 B到直线CD的距离的比值为λ,则函数f(x)=cos2x+2λsinx的最大值与最小值之和为( )| A. | $-\frac{3}{2}$ | B. | $-\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{2}$ |