题目内容
1.已知公比为q(q≠1),的等比数列{an}的前n项和为Sn,则数列{$\frac{1}{{a}_{n}}$}的前n项和为( )| A. | $\frac{{q}^{n}}{{S}_{n}}$ | B. | $\frac{{S}_{n}}{{q}^{n}}$ | C. | $\frac{1}{{S}_{n}{q}^{n-1}}$ | D. | $\frac{{S}_{n}}{{a}_{{1}^{2}}{q}^{n-1}}$ |
分析 根据等比数列的前n项和公式进行计算即可.
解答 解:∵{an}是公比为q(q≠1)的等比数列,
∴数列{$\frac{1}{{a}_{n}}$}是公比为$\frac{1}{q}$(q≠1)的等比数列,首项为$\frac{1}{{a}_{1}}$,
则数列{$\frac{1}{{a}_{n}}$}的前n项和为Tn=$\frac{\frac{1}{{a}_{1}}(1-(\frac{1}{q})^{n})}{1-\frac{1}{q}}$=$\frac{q({q}^{n}-1)}{{{a}_{1}q}^{n}(q-1)}$=$\frac{{a}_{1}•\frac{1-{q}^{n}}{1-q}}{{{a}_{1}}^{2}{q}^{n-1}}$=$\frac{{S}_{n}}{{a}_{{1}^{2}}{q}^{n-1}}$,
故选:D.
点评 本题主要考查等比数列前n项和公式的应用,根据条件判断数列是等比数列是解决本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
4.李华经营了两家电动轿车销售连锁店.其月利润(单位:x元)分别为L1=-5x2+900x-16000,L2=300x-2000(其中x为销售辆数).若某月两连锁店共销售了110辆.则能获得的最大利润为( )
| A. | 11000 | B. | 22000 | C. | 33000 | D. | 40000 |
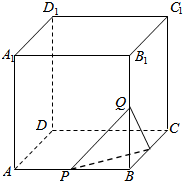 如图所示,P、Q、R分别是正方形的棱AB、BB1、BC的中点,则BD1与平面PQR的位置关系是BD1⊥平面PQR.
如图所示,P、Q、R分别是正方形的棱AB、BB1、BC的中点,则BD1与平面PQR的位置关系是BD1⊥平面PQR.