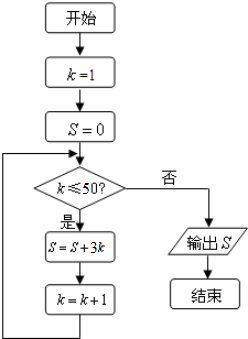
题目内容
8.口袋里装有大小相同的3个白球和2个黑球,每次从中不放回随机抽取1个球,连续抽出2次,则在第一次抽到白球的条件下,第二次抽到白球的概率为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 设已知第一次取出的是白球为事件A,第二次也取到白球为事件B,先求出n(A),n(AB)的种数,然后利用条件概率公式进行计算即可.
解答 解:设第一次抽到白球为事件A,第二次抽到白球为事件B,
则n(A)=${C}_{3}^{1}•{C}_{4}^{1}$=12,n(AB)=${C}_{3}^{1}•{C}_{2}^{1}$=6,
所以P(B|A)=$\frac{n(AB)}{n(A)}$=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题主要考查条件概率的求法,熟练掌握条件概率的概率公式是关键.

练习册系列答案
相关题目
18.已知命题p:?x∈R,2x-1>0,则命题?p为( )
| A. | ?x∈R,2x-1≤0 | B. | ?x∈R,2x-1≤0 | C. | ?x∈R,2x-1<0 | D. | ?x∈R,2x-1<0 |
3.在空间中,设直线l的方向向量为$\overrightarrow{a}$,平面α的法向量为$\overrightarrow{b}$,对于原命题“若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则l∥α”,下列判断正确的是( )
| A. | 原命题为真,否命题为真 | B. | 原命题为假,否命题为假 | ||
| C. | 原命题为假,否命题为真 | D. | 原命题为真,否命题为假 |
 正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2,
正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2,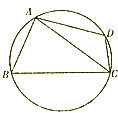 某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.
某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.