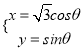题目内容
【题目】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:![]() 求出
求出![]() 的导数,当
的导数,当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增;对判别式讨论,即当
上单调递增;对判别式讨论,即当![]() 时
时![]() 时,即可求得结果
时,即可求得结果
![]() 由题意得
由题意得![]() ,
,![]() ,将问题转化为关于
,将问题转化为关于![]() 的不等式
的不等式![]() ,求导算单调性即可得出结果
,求导算单调性即可得出结果
解析:(Ⅰ)![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() ,即
,即![]() 时,由
时,由![]() 解得
解得![]() 或
或![]() ;
;
综上可知,当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调减;
上单调减;
(Ⅱ)由(Ⅰ)知,![]() 的两根为
的两根为![]() ,且
,且![]() ,
,
则![]() ,
,![]() ,由
,由![]() 知,
知,![]() ,
,
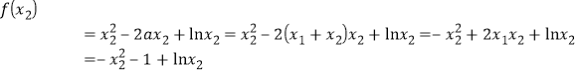 ,
,
不等式![]() 可化为
可化为![]() ,即
,即![]() ,
,
令![]() ,
,![]() ,
,
由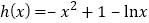 在
在![]() 上单调递减,且
上单调递减,且![]() ,则
,则![]() 的解为
的解为![]() ,
,
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,则
上单调递减,则![]() ,
,
依题知![]() ,所以
,所以![]()

【题目】为了响应厦门市政府“低碳生活,绿色出行”的号召,思明区委文明办率先全市发起“少开一天车,呵护厦门蓝”绿色出行活动.“从今天开始,从我做起,力争每周至少一天不开车,上下班或公务活动带头选择步行、骑车或乘坐公交车,鼓励拼车……”铿锵有力的话语,传递了绿色出行、低碳生活的理念.
某机构随机调查了本市部分成年市民某月骑车次数,统计如下:
年龄 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
18岁至31岁 | 8 | 12 | 20 | 60 | 140 | 150 |
32岁至44岁 | 12 | 28 | 20 | 140 | 60 | 150 |
45岁至59岁 | 25 | 50 | 80 | 100 | 225 | 450 |
60岁及以上 | 25 | 10 | 10 | 18 | 5 | 2 |
联合国世界卫组织于2013年确定新的年龄分段:44岁及以下为青年人,45岁至59岁为中年人,60岁及以上为老年人.用样本估计总体的思想,解决如下问题:
(1)估计本市一个18岁以上青年人每月骑车的平均次数;
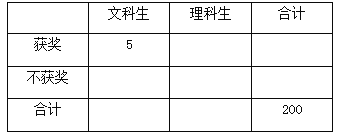
(2)若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()