题目内容
【题目】已知函数![]() 若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(﹣x2);(2)f(x2)>f(﹣x1);(3)f(x1)>f(﹣x1);(4)f(x2)>f(﹣x2).正确的个数为( )
若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(﹣x2);(2)f(x2)>f(﹣x1);(3)f(x1)>f(﹣x1);(4)f(x2)>f(﹣x2).正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】函数f(x)的定义域为R.
f′(x)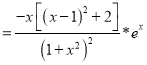 ,
,
当x<0时,f′(x)>0;当x>0时,f′(x)<0.
∴函数f(x)的单调递增区间为(﹣∞,0),单调递减区间为(0,+∞).
由f(x1)=f(x2),且x1<x2,可知x1<0,x2>0,
当x<1时,由于![]() >0,ex>0,得到f(x)>0;同理,当x>1时,f(x)<0.
>0,ex>0,得到f(x)>0;同理,当x>1时,f(x)<0.
由上可知:x1∈(﹣∞,0),x2∈(0,1).
下面证明:x∈(0,1),f(x)<f(﹣x),
即证![]() <
<![]() .
.
此不等式等价于![]() .
.
令g(x)=![]() ,则g′(x)=﹣xe﹣x(e2x﹣1).
,则g′(x)=﹣xe﹣x(e2x﹣1).
当x∈(0,1)时,g′(x)<0,g(x)单调递减,
∴g(x)<g(0)=0.
即![]() .
.
∴x∈(0,1),f(x)<f(﹣x).
由x1∈(﹣∞,0),可知f(x1)<f(﹣x2),故(1)错误;
f(x1)>f(﹣x1),故(3)正确;
由x2∈(0,1),可知f(x2)>f(﹣x1),故(2)正确;
f(x2)<f(﹣x2),故(4)错误.
∴正确命题的个数是2个.
故选:B.

【题目】下表是一位母亲给儿子作的成长记录:
年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
根据以上样本数据,她建立了身高 ![]() (cm)与年龄x(周岁)的线性回归方程为
(cm)与年龄x(周岁)的线性回归方程为 ![]() ,给出下列结论:
,给出下列结论:
①y与x具有正的线性相关关系;
②回归直线过样本的中心点(42,117.1);
③儿子10岁时的身高是 ![]() cm;
cm;
④儿子年龄增加1周岁,身高约增加 ![]() cm.
cm.
其中,正确结论的个数是
A.1
B.2
C.3
D.4
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
参考公式及数据: 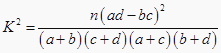
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由?