Question

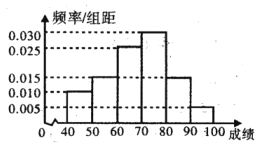
【题目】在某校矩形的航天知识竞赛中，参与竞赛的文科生与理科生人数之比为1：3，且成绩分布在范围内，规定分数在80以上（含80）的同学获奖，按文理科用分层抽样的放发抽取200人的成绩作为样本，得到成绩的频率分布直方图.

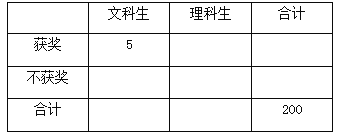
(Ⅰ)填写下面的列联表，能否有超过95%的把握认为“获奖与学生的文理科有关”；

(Ⅱ)将上述调查所得的频率视为概率，现从参赛学生中，任意抽取3名学生，记“获奖”学生人数为,求的分布列及数学期望.

附表及公式：，其中

Answer 1

【答案】(1) 有超过 95%的把握认为“获奖与学生的文理科有关”(2)见解析

【解析】试题分析：（1）列出表格根据公式计算出K2，参考表格即可得出结论．（2）由表中数据可知，抽到获奖同学的概率为，将频率视为概率，所以X可取0，1，2，3，且X～B（3，）．即可得出．

解析：

(Ⅰ)联表如下：

由表中数据可得：

所以有超过 95%的把握认为“获奖与学生的文理科有关”

（Ⅱ）由表中数据可知，抽到获奖学生的概率为

将频率视为概率，所以可取且

期望.