题目内容
(本小题满分14分)
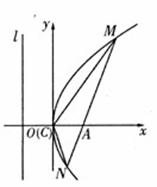
已知直线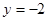 上有一个动点
上有一个动点 ,过点
,过点 作直线
作直线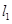 垂直于
垂直于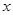 轴,动点
轴,动点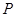 在
在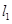 上,且满足
上,且满足
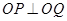 (
(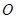 为坐标原点),记点
为坐标原点),记点 的轨迹为
的轨迹为 .
.
(1)求曲线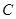 的方程;
的方程;
(2)若直线 是曲线
是曲线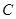 的一条切线, 当点
的一条切线, 当点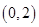 到直线
到直线 的距离最短时,求直线
的距离最短时,求直线 的方程.
的方程.
已知直线
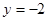 上有一个动点
上有一个动点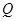 ,过点
,过点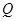 作直线
作直线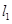 垂直于
垂直于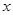 轴,动点
轴,动点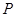 在
在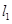 上,且满足
上,且满足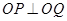 (
(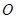 为坐标原点),记点
为坐标原点),记点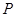 的轨迹为
的轨迹为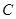 .
.(1)求曲线
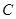 的方程;
的方程;(2)若直线
 是曲线
是曲线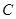 的一条切线, 当点
的一条切线, 当点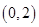 到直线
到直线 的距离最短时,求直线
的距离最短时,求直线 的方程.
的方程. (1)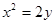
 . (2)
. (2) 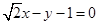 或
或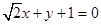 .
.
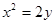
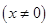 . (2)
. (2) 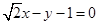 或
或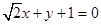 .
.本试题主要是考查了轨迹方程的求解,以及直线与抛物线位置关系的综合运用。
(1)设点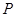 的坐标为
的坐标为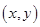 ,则点
,则点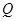 的坐标为
的坐标为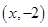 .
.
∵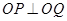 , ∴
, ∴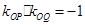 ,得到关系式。
,得到关系式。
(2)直线 与曲线
与曲线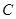 相切,∴直线
相切,∴直线 的斜率存在.
的斜率存在.
设直线 的方程为
的方程为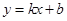 ,与抛物线联立方程组,结合韦达定理和点到直线的距离公式得到结论。
,与抛物线联立方程组,结合韦达定理和点到直线的距离公式得到结论。
(1)解:设点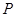 的坐标为
的坐标为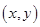 ,则点
,则点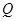 的坐标为
的坐标为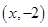 .
.
∵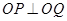 , ∴
, ∴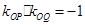 .
.
当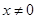 时,得
时,得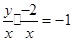 ,化简得
,化简得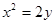 . …… 2分
. …… 2分
当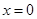 时,
时, 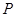 、
、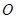 、
、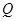 三点共线,不符合题意,故
三点共线,不符合题意,故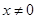 .
.
∴曲线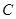 的方程为
的方程为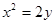
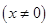 . …… 4分
. …… 4分
(2) 解法1:∵ 直线 与曲线
与曲线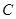 相切,∴直线
相切,∴直线 的斜率存在.
的斜率存在.
设直线 的方程为
的方程为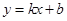 , …… 5分
, …… 5分
由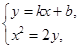 得
得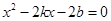 .
.
∵ 直线 与曲线
与曲线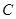 相切,
相切,
∴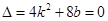 ,即
,即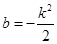 . …… 6分
. …… 6分
点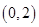 到直线
到直线 的距离
的距离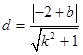
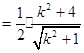 …… 7分
…… 7分
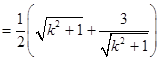 …… 8分
…… 8分
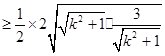 …… 9分
…… 9分
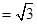 . …… 10分
. …… 10分
当且仅当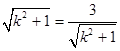 ,即
,即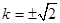 时,等号成立.此时
时,等号成立.此时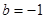 . ……12分
. ……12分
∴直线 的方程为
的方程为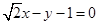 或
或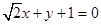 . …… 14分
. …… 14分
解法2:利用导数求切线。
(1)设点
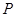 的坐标为
的坐标为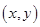 ,则点
,则点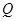 的坐标为
的坐标为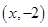 .
.∵
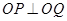 , ∴
, ∴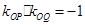 ,得到关系式。
,得到关系式。(2)直线
 与曲线
与曲线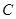 相切,∴直线
相切,∴直线 的斜率存在.
的斜率存在.设直线
 的方程为
的方程为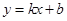 ,与抛物线联立方程组,结合韦达定理和点到直线的距离公式得到结论。
,与抛物线联立方程组,结合韦达定理和点到直线的距离公式得到结论。(1)解:设点
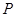 的坐标为
的坐标为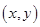 ,则点
,则点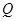 的坐标为
的坐标为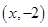 .
.∵
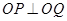 , ∴
, ∴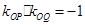 .
. 当
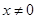 时,得
时,得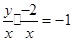 ,化简得
,化简得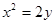 . …… 2分
. …… 2分当
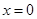 时,
时, 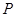 、
、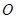 、
、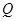 三点共线,不符合题意,故
三点共线,不符合题意,故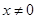 .
.∴曲线
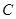 的方程为
的方程为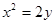
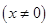 . …… 4分
. …… 4分(2) 解法1:∵ 直线
 与曲线
与曲线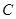 相切,∴直线
相切,∴直线 的斜率存在.
的斜率存在.设直线
 的方程为
的方程为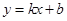 , …… 5分
, …… 5分由
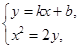 得
得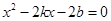 .
.∵ 直线
 与曲线
与曲线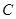 相切,
相切,∴
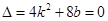 ,即
,即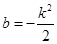 . …… 6分
. …… 6分点
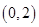 到直线
到直线 的距离
的距离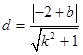
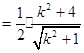 …… 7分
…… 7分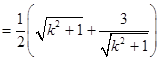 …… 8分
…… 8分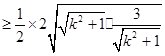 …… 9分
…… 9分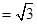 . …… 10分
. …… 10分当且仅当
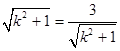 ,即
,即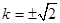 时,等号成立.此时
时,等号成立.此时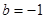 . ……12分
. ……12分∴直线
 的方程为
的方程为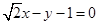 或
或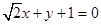 . …… 14分
. …… 14分解法2:利用导数求切线。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点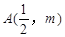 ,
, 点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设
点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设 为抛物线上的一个定点,过
为抛物线上的一个定点,过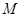 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦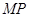 ,
,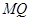 ,求证:
,求证: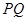 恒过定点
恒过定点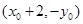 .(3)直线
.(3)直线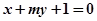 与抛物线交于
与抛物线交于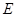 ,
,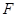 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点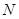 ,使得△
,使得△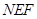 为以
为以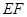 为斜边的直角三角形.
为斜边的直角三角形.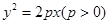 的焦点为
的焦点为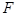 ,点
,点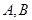 在抛物线上,且
在抛物线上,且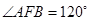 ,过弦
,过弦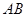 中点
中点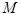 作准线
作准线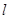 的垂线,垂足为
的垂线,垂足为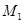 ,则
,则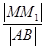 的最大值为_________.
的最大值为_________.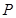 是抛物线
是抛物线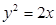 上的动点,
上的动点,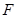 是抛物线的焦点,若点
是抛物线的焦点,若点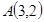 ,则
,则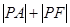 的最小值是 .
的最小值是 .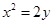 的焦点到准线的距离为( )
的焦点到准线的距离为( )
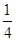
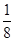
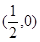 的距离与P到直线
的距离与P到直线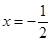 距离相等
距离相等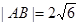 ,求直线l的方程;
,求直线l的方程;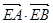 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由. 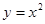 上的点M(
上的点M(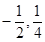 )的切线的倾斜角为( )
)的切线的倾斜角为( )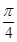
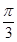

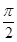
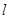 (南北向)旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路
(南北向)旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路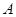 处的距离相等,并在湖中建造一个三角形的游乐区
处的距离相等,并在湖中建造一个三角形的游乐区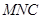 ,三个顶点
,三个顶点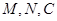 都在湖沿岸上,直线通道
都在湖沿岸上,直线通道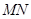 经过
经过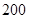 米处,
米处,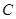 在
在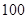 米处,现以点
米处,现以点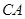 所在直线为
所在直线为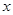 轴建立平面直角坐标系,
轴建立平面直角坐标系,