题目内容
如图,某旅游区拟在公路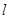 (南北向)旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路
(南北向)旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路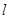 的距离与到
的距离与到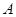 处的距离相等,并在湖中建造一个三角形的游乐区
处的距离相等,并在湖中建造一个三角形的游乐区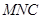 ,三个顶点
,三个顶点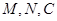 都在湖沿岸上,直线通道
都在湖沿岸上,直线通道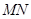 经过
经过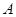 处.经测算,
处.经测算,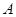 在公路
在公路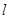 正东方向
正东方向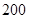 米处,
米处,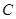 在
在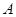 的正西方向
的正西方向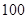 米处,现以点
米处,现以点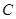 为坐标原点,以线段
为坐标原点,以线段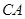 所在直线为
所在直线为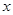 轴建立平面直角坐标系,
轴建立平面直角坐标系,
(1)求抛物线的方程
(2)试确定直线通道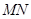 的位置,使得三角形游乐区
的位置,使得三角形游乐区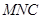 的面积最小,并求出最小值
的面积最小,并求出最小值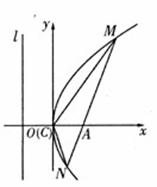
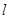 (南北向)旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路
(南北向)旁开发一个抛物线形的人工湖,湖沿岸上每一点到公路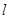 的距离与到
的距离与到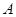 处的距离相等,并在湖中建造一个三角形的游乐区
处的距离相等,并在湖中建造一个三角形的游乐区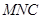 ,三个顶点
,三个顶点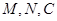 都在湖沿岸上,直线通道
都在湖沿岸上,直线通道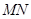 经过
经过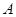 处.经测算,
处.经测算,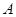 在公路
在公路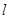 正东方向
正东方向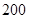 米处,
米处,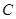 在
在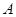 的正西方向
的正西方向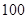 米处,现以点
米处,现以点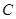 为坐标原点,以线段
为坐标原点,以线段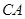 所在直线为
所在直线为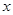 轴建立平面直角坐标系,
轴建立平面直角坐标系,(1)求抛物线的方程
(2)试确定直线通道
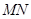 的位置,使得三角形游乐区
的位置,使得三角形游乐区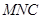 的面积最小,并求出最小值
的面积最小,并求出最小值
(1)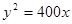 (2)当
(2)当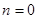 时,即
时,即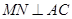 时,
时,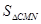 取得最小值
取得最小值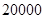
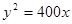 (2)当
(2)当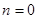 时,即
时,即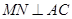 时,
时,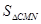 取得最小值
取得最小值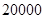
(1)因为抛物线的开口向右,所以可设其方程为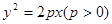 ,
,
再根据焦点坐标,可确定抛物线方程.
(2)设直线MN的方程为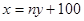 ,它与抛物线方程联立,消x后得到关于y的一元二次方程,利用弦长公式求出高的值,然后再求出|AC|的值,进而求出
,它与抛物线方程联立,消x后得到关于y的一元二次方程,利用弦长公式求出高的值,然后再求出|AC|的值,进而求出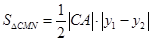 .
.
(1)依题意,设所求的抛物线方程为: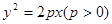 ………1分
………1分
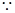 抛物线的焦点
抛物线的焦点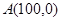 ,
,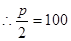 ,故所求的方程为:
,故所求的方程为: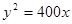 …4分
…4分
(2)设点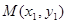 ,
,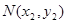 ,直线
,直线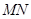 的方程为:
的方程为: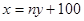
联立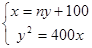 消去
消去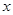 ,得;
,得;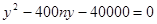 …6分
…6分
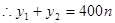 ,
,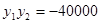 …7分
…7分
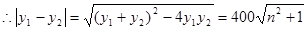 …9分
…9分
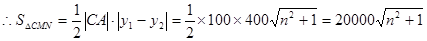 …11分
…11分
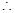 当
当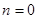 时,即
时,即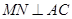 时,
时,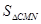 取得最小值
取得最小值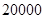
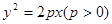 ,
,再根据焦点坐标,可确定抛物线方程.
(2)设直线MN的方程为
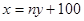 ,它与抛物线方程联立,消x后得到关于y的一元二次方程,利用弦长公式求出高的值,然后再求出|AC|的值,进而求出
,它与抛物线方程联立,消x后得到关于y的一元二次方程,利用弦长公式求出高的值,然后再求出|AC|的值,进而求出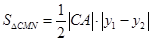 .
.(1)依题意,设所求的抛物线方程为:
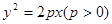 ………1分
………1分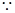 抛物线的焦点
抛物线的焦点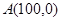 ,
,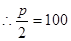 ,故所求的方程为:
,故所求的方程为: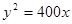 …4分
…4分(2)设点
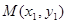 ,
,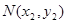 ,直线
,直线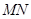 的方程为:
的方程为: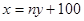
联立
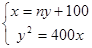 消去
消去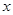 ,得;
,得;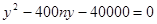 …6分
…6分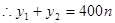 ,
,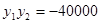 …7分
…7分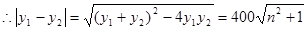 …9分
…9分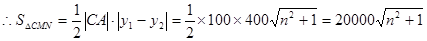 …11分
…11分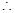 当
当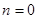 时,即
时,即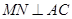 时,
时,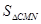 取得最小值
取得最小值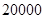

练习册系列答案
相关题目
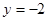 上有一个动点
上有一个动点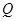 ,过点
,过点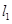 垂直于
垂直于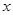 轴,动点
轴,动点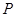 在
在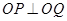 (
(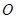 为坐标原点),记点
为坐标原点),记点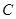 .
. 是曲线
是曲线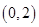 到直线
到直线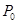 是抛物线
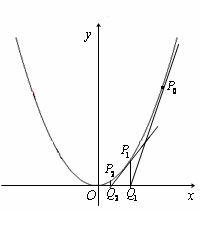
是抛物线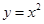 上一点,且在第一象限. 过点
上一点,且在第一象限. 过点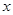 轴于
轴于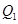 点,过
点,过 点,此时就称
点,此时就称 ,
, .记
.记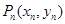 ,
,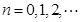 。
。
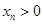 ;
;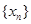 为单调递减数列;
为单调递减数列;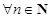 ,
,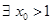 ,使得
,使得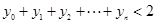 .
.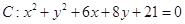 ,抛物线
,抛物线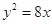 的准线为
的准线为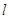 ,设抛物线上任意一点
,设抛物线上任意一点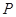 到直线
到直线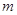 ,则
,则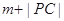 的最小值为
的最小值为 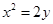 上两点,点P,Q的横坐标分别为4,
上两点,点P,Q的横坐标分别为4,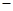 2,过P、Q分别作抛物线的切线,两切线交于A,则点A的纵坐标为__________。
2,过P、Q分别作抛物线的切线,两切线交于A,则点A的纵坐标为__________。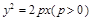 焦点的直线与抛物线交于
焦点的直线与抛物线交于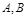 两点,
两点,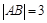 ,且AB中点的纵坐标为
,且AB中点的纵坐标为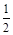 ,则
,则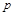 的值为 .
的值为 .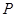 是抛物线
是抛物线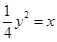 上一个动点,则点
上一个动点,则点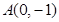 的距离与点
的距离与点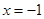 的距离和的最小值是 。
的距离和的最小值是 。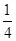
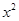 的焦点坐标是______________.
的焦点坐标是______________.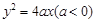 的焦点坐标是( )
的焦点坐标是( )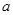 , 0)
, 0)