题目内容
抛物线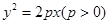 的焦点为
的焦点为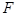 ,点
,点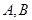 在抛物线上,且
在抛物线上,且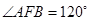 ,过弦
,过弦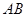 中点
中点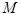 作准线
作准线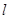 的垂线,垂足为
的垂线,垂足为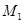 ,则
,则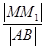 的最大值为_________.
的最大值为_________.
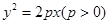 的焦点为
的焦点为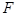 ,点
,点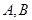 在抛物线上,且
在抛物线上,且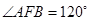 ,过弦
,过弦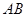 中点
中点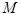 作准线
作准线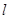 的垂线,垂足为
的垂线,垂足为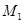 ,则
,则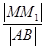 的最大值为_________.
的最大值为_________.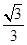
试题分析:解:设AF=a,BF=b,由抛物线定义,2|MM1|=a+b.而余弦定理,|AB|2=a2+b2-2abcos120°=(a+b)2-ab,
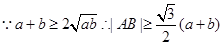 ,所以
,所以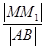 的最大值为
的最大值为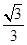 。
。点评:本题主要考查抛物线的应用和余弦定理的应用.考查了学生综合分析问题和解决问题的能力

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
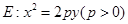 的焦点F作斜率分别为
的焦点F作斜率分别为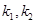 的两条不同的直线
的两条不同的直线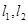 ,且
,且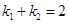 ,
,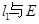 相交于点A,B,
相交于点A,B,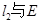 相交于点C,D。以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为
相交于点C,D。以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为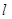 。
。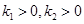 ,证明;
,证明;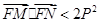 ;
;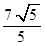 ,求抛物线E的方程。
,求抛物线E的方程。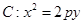 (
(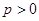 )上一点
)上一点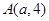 到其准线的距离为
到其准线的距离为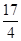 .
.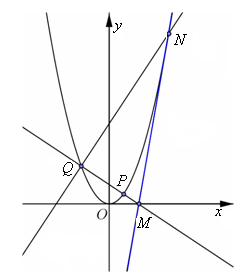
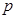 与
与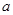 的值;
的值;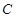 上动点
上动点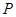 的横坐标为
的横坐标为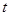 (
(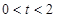 ),过点
),过点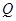 ,交
,交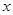 轴于
轴于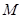 点(直线
点(直线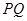 的斜率记作
的斜率记作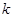 ).过点
).过点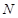 .若
.若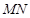 恰好是
恰好是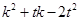 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.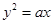 的焦点到准线的距离为4,则此抛物线的焦点坐标为
的焦点到准线的距离为4,则此抛物线的焦点坐标为


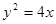 及点
及点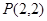 ,直线
,直线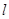 的斜率为1且不过点P,与抛物线交于A,B两点。
的斜率为1且不过点P,与抛物线交于A,B两点。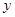 轴上截距的取值范围;
轴上截距的取值范围;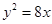 上一点P到y轴的距离是4,则点P到该抛物线的焦点的距离是 ( )
上一点P到y轴的距离是4,则点P到该抛物线的焦点的距离是 ( )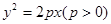 上一点
上一点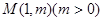 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线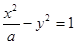 的左顶点为
的左顶点为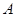 ,若双曲线的一条渐近线与直线
,若双曲线的一条渐近线与直线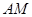 平行,则实数
平行,则实数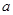 的值是( )
的值是( )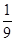
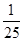
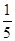
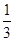
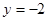 上有一个动点
上有一个动点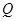 ,过点
,过点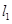 垂直于
垂直于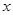 轴,动点
轴,动点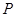 在
在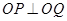 (
(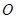 为坐标原点),记点
为坐标原点),记点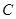 .
. 是曲线
是曲线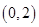 到直线
到直线