Question

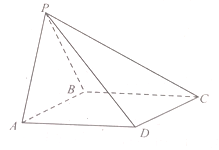
【题目】如图，在三棱锥中，平面平面， ， ．

（1）求直线与平面所成角的正弦值；

（2）若动点在底面边界及内部，二面角的余弦值为，求的最小值．

Answer 1

【答案】（1）（2）.

【解析】试题分析：（1）取AC中点O，以O为坐标原点，OB、OC、OP分别为x、y、z轴建立空间直角坐标系，用坐标表示点与向量，求出平面PBC的法向量，利用公式即可求得直线PA与平面PBC所成角的正弦值；（2）确定平面PAC的法向量，设M（m，n，0），求出平面PAM的法向量，利用，即可求得结论．

试题解析：

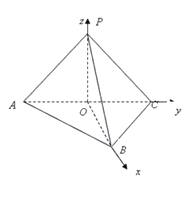
（1）取AC中点O，∵AB=BC，AP=PC，∴OB⊥OC， OP⊥OC.

∵平面ABC⊥平面APC，平面ABC∩平面APC=AC， ∴OB⊥平面PAC， ∴OB⊥OP.

以O为坐标原点，OB、OC、OP分别为 x、y、z轴建立如图所示空间直角坐标系，

∵AB=BC=PA=，∴OB=OC=OP=1，

∴，

∴

设平面PBC的法向量， 由得方程组，取，∴.

∴直线PA与平面PBC所成角的正弦值为．

（2）由题意平面PAC的法向量，设平面PAM的法向量为 ，

∵ ，

∴，取∴.

∴，∴n+1=3m或n+1=-3m（舍去）.

∴B点到AM的最小值为垂直距离.