题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,过
,过![]() 且与
且与![]() 轴垂直的直线与椭圆
轴垂直的直线与椭圆![]() 在第一象限内的交点为
在第一象限内的交点为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,当
两点,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】试题分析:(1)由题意得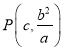 ,
, ![]() ,∴
,∴![]() .①∵
.①∵![]() ,∴
,∴![]() .②联立①②得a,b,c即得椭圆
.②联立①②得a,b,c即得椭圆![]() 的方程(2)设直线
的方程(2)设直线![]() 方程为:
方程为: ![]() ,
, ![]() 点坐标为
点坐标为![]() ,
, ![]() 点坐标为
点坐标为![]() .联立
.联立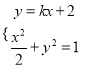 得
得![]() ,根据韦达定理由弦长公式得,
,根据韦达定理由弦长公式得, 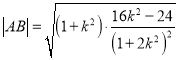 ,又点
,又点![]() 到直线
到直线![]() 的距离
的距离![]() ,
, 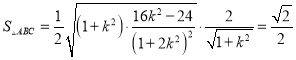 ,解得k值,即得直线
,解得k值,即得直线![]() 的方程.
的方程.
试题解析:
(1)设![]() ,
, ![]() ,则
,则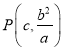 ,
,
∵![]() ,∴
,∴![]() .①
.①
∵![]() ,∴
,∴![]() .②
.②
联立①②得, ![]() ,
, ![]() ,
, ![]() .
.
∴椭圆方程为![]() .
.
(2)显然直线![]() 斜率存在,设直线
斜率存在,设直线![]() 方程为:
方程为: ![]() ,
, ![]() 点坐标为
点坐标为![]() ,
, ![]() 点坐标为
点坐标为![]() .
.
联立方程组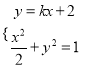 ,得
,得![]() ,
,
令![]() 得,
得, ![]() ,
,
∴![]() ,
, ![]() ,
,
由弦长公式得, ![]()
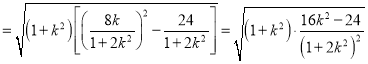 ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
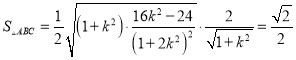 ,解得
,解得![]() .
.
∴![]() 的方程为:
的方程为: ![]() .
.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案【题目】微信是当前主要的社交应用之一,有着几亿用户,覆盖范围广,及时快捷,作为移动支付的重要形式,微信支付成为人们支付的重要方式和手段。某公司为了解人们对“微信支付”认可度,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否喜欢微信支付”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否喜欢微信支付”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
组号 | 分组 | 喜欢微信支付的人数 | 喜欢微信支付的人数 占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
第六组 |
|
|
|

(1)补全频率分布直方图,并求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)在第四、五、六组“喜欢微信支付”的人中,用分层抽样的方法抽取![]() 人参加“微信支付日鼓励金”活动,求第四、五、六组应分别抽取的人数;
人参加“微信支付日鼓励金”活动,求第四、五、六组应分别抽取的人数;
(3)在(2)中抽取的![]() 人中随机选派
人中随机选派![]() 人做采访嘉宾,求所选派的
人做采访嘉宾,求所选派的![]() 人没有第四组人的概率.
人没有第四组人的概率.
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.