题目内容
13.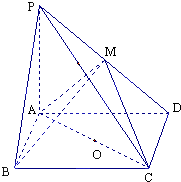 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M(1)求证:平面ABM⊥平面PCD;
(2)求直线PC与平面ABM所成的角的正弦值.
分析 (1)利用线面、面面垂直的判定定理、性质定理即可证明;
(2)通过建立空间直角坐标系,先求出平面ABM的法向量,进而即可求出线面角.
解答 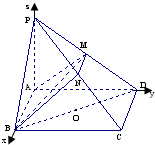 解:(1)证明:由题意,M在以BD为直径的球面上,则BM⊥PD,
解:(1)证明:由题意,M在以BD为直径的球面上,则BM⊥PD,
∵PA⊥平面ABCD,∴PA⊥AB,
又∵AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,∴AB⊥PD,
∵BM∩AB=B,
∴PD⊥平面ABM,又PD?平面PCD,
∴平面ABM⊥平面PCD.
(2)由(1)可知:PD⊥平面ABM,∴PD⊥AM,又在Rt△PAD,PA=AD,∴PM=MD.
如图所示,建立空间直角坐标系,
则A(0,0,0),P(0,0,4),B(2,0,0),C(2,4,0),D(0,4,0),M(0,2,2),
由(1)可知:$\overrightarrow{PD}$是平面ABM的一个法向量$\overrightarrow{PD}$=(0,4,-4),
又$\overrightarrow{PC}$=(2,4,-4),
设PC与平面ABM所成的角为θ,
则sinθ=|cos<$\overrightarrow{PD}$,$\overrightarrow{PC}$>|=$\frac{|\overrightarrow{PD}•\overrightarrow{PC}|}{|\overrightarrow{PD}|•|\overrightarrow{PC}|}$=$\frac{32}{\sqrt{32}•\sqrt{36}}$=$\frac{2\sqrt{2}}{3}$.
点评 熟练掌握线面、面面垂直的判定定理、性质定理及通过建立空间直角坐标系利用平面的法向量与斜向量求出线面角是解题的关键.

练习册系列答案
相关题目
4.给出下列命题
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)复数Z=a+bi(其中a、in+i-n,n∈Z)的虚部为i.
其中正确命题的序号是( )
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)复数Z=a+bi(其中a、in+i-n,n∈Z)的虚部为i.
其中正确命题的序号是( )
| A. | (1) | B. | (2)(3) | C. | (1)(3) | D. | (1)(4) |
18.对具有相关关系的两个变量统计分析的一种常用的方法是( )
| A. | 回归分析 | B. | 相关系数分析 | C. | 残差分析 | D. | 相关指数分析 |
5.已知集合A={x|x2-2x>0},B={x|-3<x<3},则( )
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |