��Ŀ����
3����ƽ��ֱ������ϵ�У���֪OΪ����ԭ�㣬��A������Ϊ��a��b������B������Ϊ��cos��x��sin��x�������Цأ�0����f��x��=$\overrightarrow{OA}•\overrightarrow{OB}$�����Ǻ���y=f��x������������С��������{an}��n��N*������a=$\sqrt{3}$��b=1����=2ʱ����{an}��ͨ�ʽ��ǰn���Sn��
���Ǻ���g��x��=2x����g��b��=g��a��•g��-2������x��Rʱ����f��x����ֵ��ΪM������ʽx2+mx��0�Ľ⼯ΪN����N⊆M����ʵ��m�����ֵ��
�������=1��a=t2��b=��1-t��2��������ʽf���ȣ�-$\sqrt{ab}$��0�������t��[0��1]���������ȵ�ȡֵ��Χ��
���� ��������֪��������������������õ�f��x���Ľ���ʽ�����л��õ�����y=f��x�������������k��ʾ��������õ�����{an}��n��N*����������Ȼ����{an}��ͨ�ʽ��ǰn���Sn��
����������ֱ��ʾ��f��x����ֵ���Լ�����ʽ�Ľ⼯������N⊆M���г�����ʽ���ʵ��m�����ֵ��
����������õ�f���ȣ�-$\sqrt{ab}$��0����һ���õ����ڦȵIJ���ʽ��������ҵ��ȼ���������
��� �⣺���������$f��x��=\overrightarrow{OA}•\overrightarrow{OB}=acos��x+bsin��x$=$\sqrt{3}cos2x+sin2x$=$2sin��2x+\frac{��}{3}��$������1�֣�
��$2sin��2x+\frac{��}{3}��=0⇒2x+\frac{��}{3}=k��⇒{x_k}=-\frac{��}{6}+\frac{k��}{2}��k��Z$������2�֣�
��k=1ʱ${x_1}=-\frac{��}{6}+\frac{��}{2}=\frac{��}{3}��0$����${x_{k+1}}-{x_k}=\frac{��}{2}$����������
��{an}Ϊ������${a_1}=\frac{��}{3}$������Ϊ$\frac{��}{2}$�ĵȲ����У�
��${a_n}=-\frac{��}{6}+\frac{n��}{2}��n��{N^*}$������3�֣�
��${S_n}=\frac{{��{a_1}+{a_n}��n}}{2}=\frac{{��\frac{��}{3}-\frac{��}{6}+\frac{n��}{2}��n}}{2}=��\frac{��}{12}+\frac{n��}{4}��n=\frac{��}{4}{n^2}+\frac{��}{12}n��n��{N^*}$������4�֣�
���� ��g��a��=g��b��+g��-2����2a=2b��2-2⇒2a=2b-2⇒b=a+2������5�֣�
��$f��x��=acos��x+bsin��x=\sqrt{{{��a+2��}^2}+{a^2}}sin����x+�գ�$��
��f��x����ֵ��Ϊ$M=[{-\sqrt{{{��a+2��}^2}+{a^2}}��\sqrt{{{��a+2��}^2}+{a^2}}}]$������6�֣�
��x2+mx=0�Ľ�Ϊ0��-m����N=[-m��0]��N=[0��-m]��
��Ҫʹ��N⊆M����$-m��[{-\sqrt{{{��a+2��}^2}+{a^2}}��\sqrt{{{��a+2��}^2}+{a^2}}}]$������7�֣�
��$\sqrt{{{��a+2��}^2}+{a^2}}=\sqrt{2{{��a+1��}^2}+2}��\sqrt{2}$����$M=[{-\sqrt{2}��\sqrt{2}}]$��
��$-\sqrt{2}��-m��\sqrt{2}$����$-\sqrt{2}��m��\sqrt{2}$��
��ʵ��m�����ֵΪ$\sqrt{2}$������8�֣�
���������$f���ȣ�-\sqrt{ab}$=t2cos��+��1-t��2sin��-t��1-t��=��1+sin��+cos�ȣ�t2-��2sin��+1��t+sin��
������ȼ��ڣ�1+sin��+cos�ȣ�t2-��2sin��+1��t+sin�ȣ�0�������t��[0��1]�������
��t=0��t=1����sin�ȣ�0��cos�ȣ�0������9�֣�
��1+2sin�ȣ�2+2sin��+2cos�ȣ�
��Գ���$t=\frac{1+2sin��}{2+2sin��+2cos��}��1$�������
��Գ����������䣨0��1���ڣ�����10�֣�
������ȼ���$\left\{\begin{array}{l}sin�ȣ�0\\ cos�ȣ�0\\��={��2sin��+1��^2}-4��1+sin��+cos�ȣ�sin�ȣ�0\end{array}\right.$����$\left\{\begin{array}{l}sin�ȣ�0\\ cos�ȣ�0\\ sin2�ȣ�\frac{1}{2}\end{array}\right.$������11�֣�
$⇒\left\{\begin{array}{l}2{k_1}�У��ȣ���+2{k_1}�У�{k_1}��z\\-\frac{��}{2}+2{k_2}�У��ȣ�\frac{��}{2}+2{k_2}�У�{k_2}��z\\ \frac{��}{12}+{k_3}�У��ȣ�\frac{5��}{12}+{k_3}�У�{k_3}��z\end{array}\right.$$⇒\frac{��}{12}+2{k_3}�У��ȣ�\frac{5��}{12}+2{k_3}�У�{k_3}��z$��
��ȵ�ȡֵ��Χ��$[{\frac{��}{12}+2k�У�\frac{5��}{12}+2k��}]��k��z$������12�֣�
���� ���⿼����ƽ������������������Ȳ����е�ͨ�ǰn��͵����Լ��������Ǻ����IJ���ʽ��������⣻�������⣮

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| A�� | -$\frac{4}{5}$ | B�� | $\frac{4}{5}$ | C�� | -$\frac{3}{5}$ | D�� | $\frac{3}{5}$ |
| A�� | 101011��2�� | B�� | 1210��3�� | C�� | 110��8�� | D�� | 68��12�� |
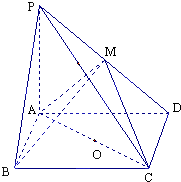 ������P-ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��PA=AD=4��AB=2����AC���е�OΪ���ġ�ACΪֱ�������潻PD�ڵ�M
������P-ABCD�У�����ABCD�Ǿ��Σ�PA��ƽ��ABCD��PA=AD=4��AB=2����AC���е�OΪ���ġ�ACΪֱ�������潻PD�ڵ�M