题目内容
3．已知函数f（x）是在R上的奇函数，而且是（0，+∞）上的减函数，证明：f（x）在（-∞，0）上是减函数？分析 由条件利用函数的单调性和奇偶性、以及不等式的性质证得f（x）在（-∞，0）上是减函数．
解答 证明：设x1＜x2＜0，则-x1＞-x2＞0，由f（x）是（0，+∞）上的减函数，可得f（-x1）＜f（-x2）．
根据f（x）为奇函数，可得-f（x1）＜-f（x2），∴f（x1）＞f（x2），
故f（x）在（-∞，0）上是减函数．
点评 本题主要考查函数的奇偶性和单调性，不等式的基本性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
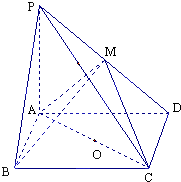在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M