题目内容
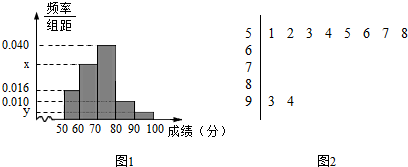
2.宜昌市“天地杯”首届中小学生汉语言文化知识电视大赛中,我校经过预赛、复赛、决赛的一路打拼,最终荣获全市一等奖的优异成绩.为选拔选手参加“汉语言文化知识电视大赛”,我校举行了一次“预选赛”活动.为了了解本次预选赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).(1)求样本容量n和频率分布直方图中的x、y的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取4名学生参加“汉语言文化知识电视大赛”,求所抽取的4名学生中至少有一人得分在[90,100]内的概率.
分析 (1)由样本容量和频数频率的关系能求出样本容量n和频率分布直方图中的x、y的值;
(2)由题意分析可知分数在[80,90)有5人,分别记为a,b,c,d,e,分数在[90,100)有2人,分别记为F,G,用列举法求得“从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学”所有的抽法方法数目以及满足条件的抽法数目,由古典概型公式计算可得答案.
解答 解:(1)根据题意:由茎叶图可知成绩在[50,60)上的有8人,其频率为0.016×10=0.16,
则样本容量n=$\frac{8}{0.16}$=50,
则y=$\frac{2}{50×10}$=0.004,
则x=0.100-0.004-0.010-0.016-0.040=0.030.
(2)由题意可知,分数在[80,90)有5人,分别记为a,b,c,d,e,
分数在[90,100)有2人,分别记为F,G.
从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有如下种情形:(a,b),(a,c),(a,d),(a,e),(a,F),(a,G),(b,c),(b,d),(b,e),(b,F),(b,G),(c,d),(c,e),(c,F),(c,G),(d,e),(d,F),(d,G),(e,F),(e,G),(F,G),共有21个基本事件;
其中所抽取的4名学生中至少有一人得分在[90,100]内有:(a,F),(a,G),(b,F),(b,G),(c,F),(c,G),(d,F),(d,G),(e,F),(e,G),(F,G),共有9个基本事件;
则所抽取的4名学生中至少有一人得分在[90,100]内的概率为P=$\frac{9}{21}$=$\frac{3}{7}$.
点评 本题主要考查等可能事件的概率,频率分布直方图的应用,解题是注意充分利用频率分布直方图分析数据.

| A. | 101011(2) | B. | 1210(3) | C. | 110(8) | D. | 68(12) |
| A. | 28 | B. | 76 | C. | 123 | D. | 199 |
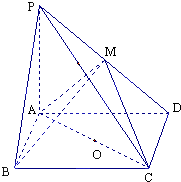 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M