题目内容
4.给出下列命题(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)复数Z=a+bi(其中a、in+i-n,n∈Z)的虚部为i.
其中正确命题的序号是( )
| A. | (1) | B. | (2)(3) | C. | (1)(3) | D. | (1)(4) |
分析 利用复数的相关概念以及性质分别分析解答.
解答 解:对于(1),根据共轭复数的概念可知,实数的共轭复数一定是实数;正确;
对于(2),满足|z-i|+|z+i|=2的复数z点的轨迹是一条线段;故(2)错误;
对于(3),若m∈Z,i2=-1,则im+im+1+im+2+im+3=im(1+i-1-i)=0;正确
对于(4),复数Z=a+bi(其中a、in+i-n,n∈Z)的虚部为b,i是虚数单位.故(4)错误.
故选:C.
点评 本题考查了复数的基本概念和虚数单位的性质运用;属于基础题.

练习册系列答案
相关题目
14.与点A(1,2)距离为1,同时与点B(3,-1)距离为2的直线的条数为( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
12.下列各数中最小的数为( )
| A. | 101011(2) | B. | 1210(3) | C. | 110(8) | D. | 68(12) |
19.我们知道,在边长为a的正三角形内任一点到三边的距离之和为定值$\frac{{\sqrt{3}}}{2}a$,类比上述结论,在棱长为a的正四面体内任一点到其四个面的距离之和为定值,此定值为( )
| A. | $\frac{{\sqrt{6}}}{3}a$ | B. | $\frac{{\sqrt{5}}}{2}a$ | C. | $\frac{{2\sqrt{2}}}{3}a$ | D. | a |
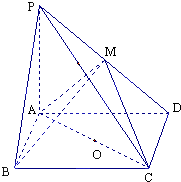 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M