题目内容
8.已知不等式$\frac{x-a}{{x}^{2}+x+1}$>$\frac{x+a}{{x}^{2}-x+1}$.(1)若不等式在R上恒成立,求实数a的取值范围;
(2)是否存在实数a使不等式的解集为(-1,4).
分析 (1)先判断分母的符号,将原不等式化简,再结合二次函数的性质从而求出a的范围;
(2)假设存在,得到a的大致范围,求出x的解集,从而得到矛盾,假设不成立.
解答 解:(1)∵x2+x+1>0,x2-x+1>0,
∴原不等式可化为:(x2-x+1)(x-a)>(x2+x+1)(x+a),
∴(a+1)x2+a<0在R上恒成立,
令f(x)=(a+1)x2+a,
∴$\left\{\begin{array}{l}{a+1<0}\\{△=-4a(a+1)<0}\end{array}\right.$,解得:a<-1;
当a=-1时,f(x)=-1<0在R上恒成立,
综上:a≤-1.
(2)由(1)得:原不等式为:(a+1)x2+a<0,①
若存在实数a使不等式的解集为(-1,4),
则$\left\{\begin{array}{l}{a<0}\\{a+1>0}\end{array}\right.$,即-1<a<0,
解不等式①得:-$\sqrt{\frac{a}{a+1}}$<x<$\sqrt{\frac{a}{a+1}}$,
∴$\sqrt{\frac{a}{a+1}}$=1或4,无解,
故不存在实数a使不等式的解集为(-1,4).
点评 本题考查了解不等式问题,考查函数恒成立问题,是一道中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
19.我们知道,在边长为a的正三角形内任一点到三边的距离之和为定值$\frac{{\sqrt{3}}}{2}a$,类比上述结论,在棱长为a的正四面体内任一点到其四个面的距离之和为定值,此定值为( )
| A. | $\frac{{\sqrt{6}}}{3}a$ | B. | $\frac{{\sqrt{5}}}{2}a$ | C. | $\frac{{2\sqrt{2}}}{3}a$ | D. | a |
3.锐角△ABC中,已知$a=\sqrt{3},A=\frac{π}{3}$,则b2+c2+bc的取值范围是( )
| A. | (3,9] | B. | (5,9] | C. | (7,9] | D. | (5,7] |
17.已知f(1)=1,f(2)=3,f(3)=4,f(4)=7,f(5)=11,…,则f(10)=( )
| A. | 28 | B. | 76 | C. | 123 | D. | 199 |
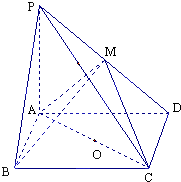 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M