题目内容
1.设a,b,c∈R,则“abc=1“是“$\frac{1}{\sqrt{a}}$+$\frac{1}{\sqrt{b}}$+$\frac{1}{\sqrt{c}}$≤a+b+c“的既不充分又不必要条件.分析 根据充分条件和必要条件的定义进行判断即可.
解答 解:若a=b=-1,c=1,满足abc=1,但$\frac{1}{\sqrt{a}}$+$\frac{1}{\sqrt{b}}$无意义,则$\frac{1}{\sqrt{a}}+\frac{1}{\sqrt{b}}+\frac{1}{\sqrt{c}}$≤a+b+c不成立.
当a=3,b=2,c=1时,$\frac{1}{\sqrt{a}}+\frac{1}{\sqrt{b}}+\frac{1}{\sqrt{c}}≤a+b+c$显然成立,但是abc=6≠1,
所以设a,b,c,∈R,则“abc=1”是“$\frac{1}{\sqrt{a}}+\frac{1}{\sqrt{b}}+\frac{1}{\sqrt{c}}≤a+b+c$”的既不充分又不必要条件.
故答案为:既不充分又不必要.
点评 本题主要考查充分条件和必要条件的判断,根据定义利用特殊值法是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知α是第三象限的角,且cos(85°+α)=$\frac{4}{5}$,则sin(α-95°)的值为( )
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
12.下列各数中最小的数为( )
| A. | 101011(2) | B. | 1210(3) | C. | 110(8) | D. | 68(12) |
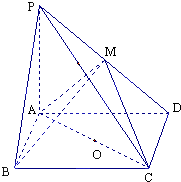 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M