题目内容

双曲线的离心率等于3，且与椭圆
x2
16
+
y2
7
=1有相同的焦点，求此双曲线方程．
因为椭圆
x2
16
+
y2
7
=1的焦点坐标为（-3，0）和（3，0），…．（2分）
则可设双曲线方程为
x2
a2
-
y2
b2
=1(a＞0，b＞0)．…（4分）
因为c=3，双曲线的离心率等于3，
所以
c
a
=3，解得a=1．…（7分）
所以b2=c2-a2=32-12=8．…（10分）
故所求双曲线方程为x2-
y2
8
=1．…．（12分）
练习册系列答案
相关题目
已知双曲线
x2
a2
-
y2
b2
=1的两条渐近线均与圆x2+y2-6x+5=0相切，且双曲线的右焦点与圆x2+y2-6x+5=0的圆心重合，则双曲线的方程是（　　）
A．
x2
5
-
y2
4
=1		B．
x2
4
-
y2
5
=1		C．
x2
6
-
y2
3
=1		D．
x2
3
-
y2
6
=1
已知双曲线C的中心在原点，焦点在坐标轴上，P（1，-2）是C上的点，且y=
2
x是C的一条渐近线，则C的方程为（　　）
A．
y2
2
-x2=1		B．2x2-
y2
2
=1
C．
y2
2
-x2=1或2x2-
y2
2
=1		D．
y2
2
-x2=1或x2-
y2
2
=1
已知P（2，1），Q（3，-2），经过P，Q两点的双曲线的标准方程为______．
从
x2
m
-
y2
n
=1（其中m，n∈{-2，-5，4}）所表示的圆锥曲线（椭圆、双曲线、抛物线）方程中任取一个，则此方程是焦点在y轴上的双曲线方程的概率为（　　）
A．
1
2
B．
4
7
C．
2
3
D．
3
4
【文科】若双曲线的渐近线方程为y=±3x，一个焦点是(0，
10
)，则双曲线的方程是______．
双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）中，F为右焦点，A为左顶点，点B（0，b）且AB⊥BF，则此双曲线的离心率为（　　）
A．
2
B．
3
C．
3
+1
2
D．
5
+1
2
若双曲线以y=±2x为渐近线，且A（1，0）为一个顶点，则双曲线的方程为（　　）
A．
x2
4
-y2=1		B．y2-
x2
4
=1		C．x2-
y2
4
=1		D．
y2
4
-x2=1
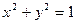动圆与两圆和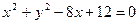都外切,则动圆圆心轨迹是  (    )
A圆        B 椭圆        C 双曲线    D 双曲线的一支

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网