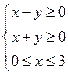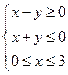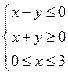题目内容
从
-
=1(其中m,n∈{-2,-5,4})所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在y轴上的双曲线方程的概率为( )
| x2 |
| m |
| y2 |
| n |
A.
| B.
| C.
| D.
|
m=-2时,n分别取-2,-5,4,能构成2个不同的圆锥曲线,
其中焦点在y轴上的双曲线方程有2个;
m=-5时,n分别取-2,-5,4,能构成2个不同的圆锥曲线,
其中焦点在y轴上的双曲线方程有2个;
m=4时,n分别取-2,-5,4,能构成3个不同的圆锥曲线,
其中焦点在y轴上的双曲线方程有0个.
∴此方程是焦点在y轴上的双曲线方程的概率为p=
=
.
故选:B.
其中焦点在y轴上的双曲线方程有2个;
m=-5时,n分别取-2,-5,4,能构成2个不同的圆锥曲线,
其中焦点在y轴上的双曲线方程有2个;
m=4时,n分别取-2,-5,4,能构成3个不同的圆锥曲线,
其中焦点在y轴上的双曲线方程有0个.
∴此方程是焦点在y轴上的双曲线方程的概率为p=
| 2+2 |
| 2+2+3 |
| 4 |
| 7 |
故选:B.

练习册系列答案
相关题目
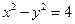 的两条渐近线与直线
的两条渐近线与直线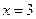 围成一个三角形区域,表示该区域的不等式组是
围成一个三角形区域,表示该区域的不等式组是