题目内容
设三位数 ,若以a,b,c为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数n有 ( )
,若以a,b,c为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数n有 ( )
 ,若以a,b,c为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数n有 ( )
,若以a,b,c为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数n有 ( )| A.45个 | B.81个 | C.165个 | D.216个 |
 C
Ca,b,c要能构成三角形的边长,显然均不为0。即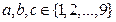
(1)若构成等边三角形,设这样的三位数的个数为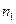 ,由于三位数中三个数码都相同,所以,
,由于三位数中三个数码都相同,所以,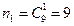 。
。
(2)若构成等腰(非等边)三角形,设这样的三位数的个数为 ,由于三位数中只有2个不同数码。设为a、b,注意到三角形腰与底可以置换,所以可取的数码组(a,b)共有
,由于三位数中只有2个不同数码。设为a、b,注意到三角形腰与底可以置换,所以可取的数码组(a,b)共有 。但当大数为底时,设a>b,必须满足
。但当大数为底时,设a>b,必须满足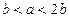 。此时,不能构成三角形的数码是
。此时,不能构成三角形的数码是
共20种情况。 同时,每个数码组(a,b)中的二个数码填上三个数位,有 种情况。
种情况。
故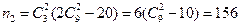 。 综上,
。 综上,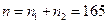 。
。
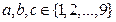
(1)若构成等边三角形,设这样的三位数的个数为
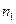 ,由于三位数中三个数码都相同,所以,
,由于三位数中三个数码都相同,所以,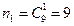 。
。(2)若构成等腰(非等边)三角形,设这样的三位数的个数为
 ,由于三位数中只有2个不同数码。设为a、b,注意到三角形腰与底可以置换,所以可取的数码组(a,b)共有
,由于三位数中只有2个不同数码。设为a、b,注意到三角形腰与底可以置换,所以可取的数码组(a,b)共有 。但当大数为底时,设a>b,必须满足
。但当大数为底时,设a>b,必须满足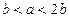 。此时,不能构成三角形的数码是
。此时,不能构成三角形的数码是| a | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| b | 4,3 2,1 | 4,3 2,1 | 3,2 1 | 3,2 1 | 1,2 | 1,2 | 1 | 1 | |
 种情况。
种情况。故
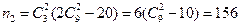 。 综上,
。 综上,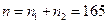 。
。
练习册系列答案
相关题目
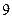 个点,其中
个点,其中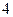 个点在一条直线上,此外无三点共线,连接这样的
个点在一条直线上,此外无三点共线,连接这样的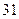 条
条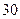 条
条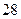 条
条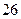 条
条 个节目,现要增加
个节目,现要增加 个节目,并要求原定的
个节目,并要求原定的