题目内容
有五张卡片,它们的正、反面分别写0与1,2与3,4与5,6与7,8与9,将其中任意三张并排放在一起组成三位数,共可组成多少个不同的三位数?
432个
解法一(间接法): 任取三张卡片可以组成不同三位数C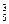 ·23·A
·23·A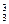 (个),其中0在百位的有C
(个),其中0在百位的有C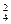 ·22·A
·22·A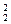 (个),这是不合题意的,故共有不同三位数
(个),这是不合题意的,故共有不同三位数 C
C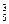 ·23·A
·23·A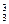 -C
-C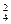 ·22·A
·22·A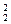 =432(个).
=432(个).
解法二 (直接法) : 第一类: 0与1卡片放首位,可以组成不同三位数有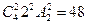 (个); 第二类: 0与1卡片不放首位,可以组成不同三位数有
(个); 第二类: 0与1卡片不放首位,可以组成不同三位数有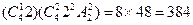 (个).
(个).
故共有不同三位数 48+384=432(个).
48+384=432(个).
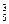 ·23·A
·23·A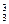 (个),其中0在百位的有C
(个),其中0在百位的有C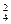 ·22·A
·22·A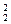 (个),这是不合题意的,故共有不同三位数
(个),这是不合题意的,故共有不同三位数 C
C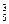 ·23·A
·23·A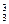 -C
-C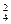 ·22·A
·22·A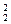 =432(个).
=432(个). 解法二 (直接法) : 第一类: 0与1卡片放首位,可以组成不同三位数有
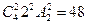 (个); 第二类: 0与1卡片不放首位,可以组成不同三位数有
(个); 第二类: 0与1卡片不放首位,可以组成不同三位数有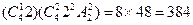 (个).
(个).故共有不同三位数
 48+384=432(个).
48+384=432(个).
练习册系列答案
相关题目
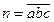 ,若以a,b,c为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数n有 ( )
,若以a,b,c为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数n有 ( )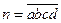 的各位数码
的各位数码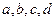 中,任三个数码皆可构成一个三角形的三条边长,则称
中,任三个数码皆可构成一个三角形的三条边长,则称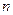 为四位三角形数,试求所有四位三角形数的个数.
为四位三角形数,试求所有四位三角形数的个数.  个数为
个数为 ,若
,若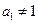 ,
,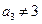 ,
, ,
, ,则不同的排列方法种数为( )
,则不同的排列方法种数为( )