题目内容
【题目】已知
为抛物线
的焦点，
为其标准线与
轴的交点，过的直线交抛物线
于
，
两点，
为线段
的中点，且
，则
__________．
【答案】8.
【解析】分析：求得抛物线的焦点和准线方程，可得E的坐标，设过F的直线为y=k（x-1），代入抛物线方程y2=4x，运用韦达定理和中点坐标公式，可得M的坐标，运用两点的距离公式可得k，再由抛物线的焦点弦公式，计算可得所求值．
详解：F（1，0）为抛物线C：y2=4x的焦点，
E（-1，0）为其准线与x轴的交点，
设过F的直线为y=k（x-1），
代入抛物线方程y2=4x，可得
k2x2-（2k2+4）x+k2=0，
设A（x1，y1），B（x2，y2），
则
中点
解得k2=1，则x1+x2=6，由抛物线的定义可得|AB|=x1+x2+2=8，故答案为8.
教材全解字词句篇系列答案
【题目】由中央电视台综合频道（
）和唯众传媒联合制作的《开讲啦》是中国首档青春电视公开课。每期节目由一位知名人士讲述自己的故事，分享他们对于生活和生命的感悟，给予中国青年现实的讨论和心灵的滋养，讨论青年们的人生问题，同时也在讨论青春中国的社会问题，受到青年观众的喜爱，为了了解观众对节目的喜爱程度，电视台随机调查了
、
两个地区的100名观众，得到如下的
列联表：
非常满意 | 满意 | 合计 | |
| 30 |
| |
|
|
| |
合计 |
已知在被调查的100名观众中随机抽取1名，该观众是地区当中“非常满意”的观众的概率为
，且
.
（Ⅰ）现从100名观众中用分层抽样的方法抽取20名进行问卷调查，则应抽取“满意”的、地区的人数各是多少；
（Ⅱ）完成上述表格，并根据表格判断是否有
的把握认为观众的满意程度与所在地区有关系；
（Ⅲ）若以抽样调查的频率为概率，从地区随机抽取3人，设抽到的观众“非常满意”的人数为
，求的分布列和期望.
|
|
|
|
|
|
|
|
|
|
附：参考公式：
【题目】为了更好地规划进货的数量，保证蔬菜的新鲜程度，某蔬菜商店从某一年的销售数据中，随机抽取了8组数据作为研究对象，如表所示（
（吨）为买进蔬菜的数量，
（天）为销售天数）：
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（1）根据上表数据在所给坐标系中绘制散点图，并用最小二乘法求出关于的线性回归方程
；
（2）根据（Ⅰ）中的计算结果，该蔬菜商店准备一次性买进25吨，预计需要销售多少天？
（参考数据和公式：
，
，
，
，
，
.）
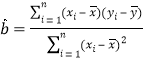
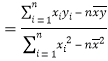