题目内容
19.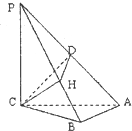 三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )
三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
分析 先证出△CHD是直角三角形,再利用基本不等式得出CH=DH=$\sqrt{2}$时△CDH的面积最大;
再利用三角形的等积法求出BC的值.
解答 解:三棱锥P-ABC中,PC⊥面ABC,AB?平面ABC,∴PC⊥AB;
又AB⊥BC,BC∩PC=C,
∴AB⊥平面PBC;
又CH?平面PBC,
∴AB⊥CH,
又CH⊥PB,
PB∩AB=B,
∴CH⊥平面PAB,
又DH?平面PAB,
∴CH⊥DH;
又△PAC是等腰直角三角形,且PA=4,D是PA的中点,
∴CD=$\frac{1}{2}$PA=2,
设CH=a,DH=b,
则a2+b2=CD2=4,
∴4=a2+b2≥2ab,
即$\frac{1}{2}$ab≤1,
当且仅当a=b=$\sqrt{2}$时,“=”成立,此时△CDH的面积最大;
在Rt△PBC,设BC=x,
则PB=$\sqrt{{PC}^{2}{+BC}^{2}}$=$\sqrt{{(2\sqrt{2})}^{2}{+x}^{2}}$=$\sqrt{8{+x}^{2}}$,
∴$\frac{1}{2}$PC•BC=$\frac{1}{2}$PB•CH,
即2$\sqrt{2}$•x=$\sqrt{8{+x}^{2}}$•$\sqrt{2}$;
解得x=$\frac{2\sqrt{6}}{3}$,
∴CB的长是$\frac{2\sqrt{6}}{3}$.
故选:D.
点评 本题考查了空间几何体的平行与垂直关系的应用问题,也考查了面积公式的应用问题,考查了利用基本不等式求最值的问题,是综合性题目.

练习册系列答案
相关题目
7.已知A,B为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右顶点,P为椭圆上异于A,B的任意一点,直线AP,BP分别交椭圆的直线l:x=4于点M,N,则$\overrightarrow{AM}$•$\overrightarrow{BN}$的值为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 9 |
11.曲线y=sinx+ex(其中e=2.71828…是自然对数的底数)在点(0,1)处的切线的斜率为( )
| A. | 2 | B. | 3 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
9.$\frac{27π}{4}$是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |