题目内容
20．已知z1=2-3i，z2=$\frac{3+2i}{（2+i）^{2}}$，则$\frac{{z}_{1}}{{z}_{2}}$=4-3i．分析 直接利用复数的除法的运算法则化简复数为a+bi是形式，然后求出复数的共轭复数．
解答 解：z1=2-3i，z2=$\frac{3+2i}{（2+i）^{2}}$，
则$\frac{{z}_{1}}{{z}_{2}}$=$\frac{（2-3i）（2+i）^{2}}{3+2i}$=$\frac{（2-3i）{（3+4i）}^{\;}}{3+2i}$=$\frac{18-i}{3+2i}$=$\frac{（18-i）（3-2i）}{（3+2i）3-2i）}$=4-3i．
故答案为：4-3i．
点评 本题考查复数的代数形式的混合运算，复数的共轭复数的求法，考查计算能力．
练习册系列答案
相关题目
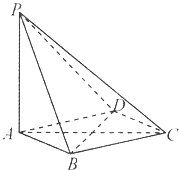如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．