题目内容
已知函数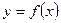 的图像是自原点出发的一条折线,当
的图像是自原点出发的一条折线,当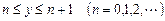 时,该图像是斜率为
时,该图像是斜率为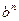 的线段(其中正常数
的线段(其中正常数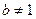 ),设数列
),设数列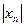 由
由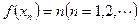 定义.
定义.
Ⅰ.求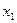 、
、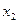 和
和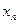 的表达式;
的表达式;
Ⅱ.求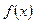 的表达式,并写出其定义域;
的表达式,并写出其定义域;
Ⅲ.证明: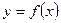 的图像与
的图像与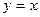 的图像没有横坐标大于1的交点.
的图像没有横坐标大于1的交点.
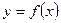 的图像是自原点出发的一条折线,当
的图像是自原点出发的一条折线,当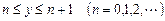 时,该图像是斜率为
时,该图像是斜率为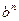 的线段(其中正常数
的线段(其中正常数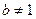 ),设数列
),设数列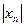 由
由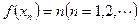 定义.
定义.Ⅰ.求
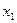 、
、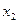 和
和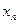 的表达式;
的表达式;Ⅱ.求
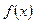 的表达式,并写出其定义域;
的表达式,并写出其定义域;Ⅲ.证明:
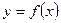 的图像与
的图像与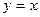 的图像没有横坐标大于1的交点.
的图像没有横坐标大于1的交点.答案见解析
Ⅰ.解:依题意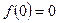 ,又由
,又由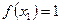 ,当
,当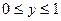 时,函数
时,函数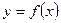 的图像是斜率为
的图像是斜率为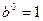 的线段,故由
的线段,故由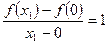 ,得
,得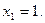
又由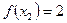 ,当
,当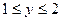 时,函数
时,函数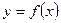 的图像是斜率为
的图像是斜率为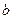 的线段,故由
的线段,故由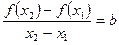 ,即
,即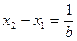 得
得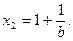
记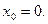 由函数
由函数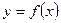 图像中第
图像中第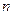 段线段的斜率为
段线段的斜率为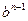 ,故得
,故得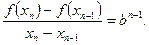
又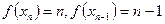 ;所以
;所以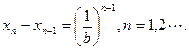
由此知数列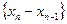 为等比数列,其首项为1,公比为
为等比数列,其首项为1,公比为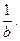 因
因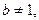 得
得
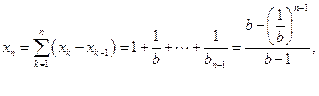 即
即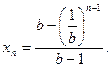
Ⅱ. 解:当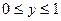 ,从Ⅰ可知
,从Ⅰ可知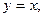 当
当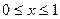 时,
时,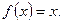
当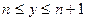 时,即当
时,即当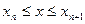 时,由Ⅰ可知
时,由Ⅰ可知
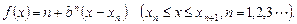
为求函数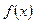 的定义域,须对
的定义域,须对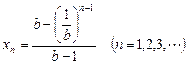 进行讨论.
进行讨论.
当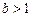 时,
时,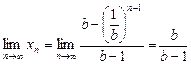 ;
;
当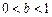 时,
时,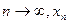 也趋向于无穷大.
也趋向于无穷大.
综上,当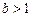 时,
时,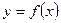 的定义域为
的定义域为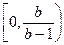 ;
;
当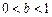 时,
时,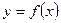 的定义域为
的定义域为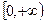 .
.
Ⅲ. 证法一:首先证明当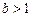 ,
,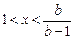 时,恒有
时,恒有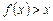 成立.
成立.
用数学归纳法证明:
(ⅰ)由Ⅱ知当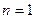 时,在
时,在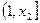 上,
上, 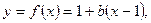
所以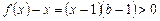 成立
成立
(ⅱ)假设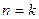 时在
时在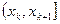 上恒有
上恒有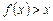 成立.
成立.
可得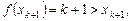
在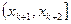 上,
上,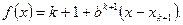
所以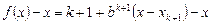
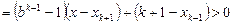 也成立.
也成立.
由(ⅰ)与(ⅱ)知,对所有自然数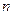 在
在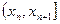 上都有
上都有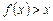 成立.
成立.
即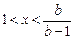 时,恒有
时,恒有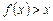 .
.
其次,当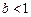 ,仿上述证明,可知当
,仿上述证明,可知当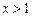 时,恒有
时,恒有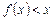 成立.
成立.
故函数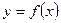 的图像与
的图像与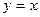 的图像没有横坐标大于1的交点.
的图像没有横坐标大于1的交点.
证法二:首先证明当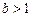 ,
,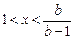 时,恒有
时,恒有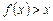 成立.
成立.
对任意的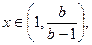 存在
存在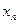 ,使
,使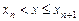 ,此时有
,此时有
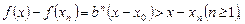
所以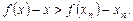
又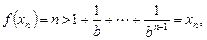 所以
所以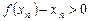 ,
,
所以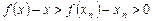 ,即有
,即有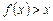 成立.
成立.
其次,当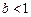 ,仿上述证明,可知当
,仿上述证明,可知当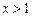 时,恒有
时,恒有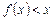 成立.
成立.
故函数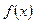 的图像与
的图像与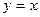 的图像没有横坐标大于1的交点.
的图像没有横坐标大于1的交点.
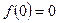 ,又由
,又由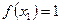 ,当
,当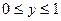 时,函数
时,函数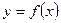 的图像是斜率为
的图像是斜率为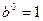 的线段,故由
的线段,故由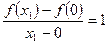 ,得
,得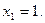
又由
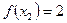 ,当
,当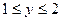 时,函数
时,函数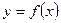 的图像是斜率为
的图像是斜率为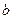 的线段,故由
的线段,故由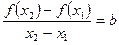 ,即
,即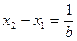 得
得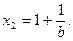
记
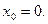 由函数
由函数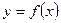 图像中第
图像中第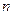 段线段的斜率为
段线段的斜率为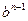 ,故得
,故得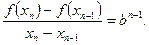
又
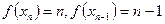 ;所以
;所以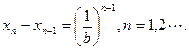
由此知数列
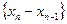 为等比数列,其首项为1,公比为
为等比数列,其首项为1,公比为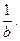 因
因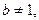 得
得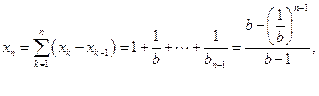 即
即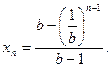
Ⅱ. 解:当
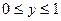 ,从Ⅰ可知
,从Ⅰ可知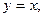 当
当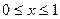 时,
时,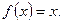
当
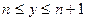 时,即当
时,即当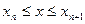 时,由Ⅰ可知
时,由Ⅰ可知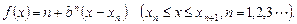
为求函数
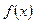 的定义域,须对
的定义域,须对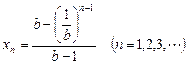 进行讨论.
进行讨论.当
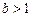 时,
时,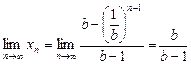 ;
;当
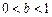 时,
时,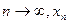 也趋向于无穷大.
也趋向于无穷大.综上,当
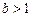 时,
时,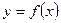 的定义域为
的定义域为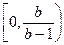 ;
;当
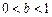 时,
时,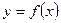 的定义域为
的定义域为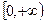 .
. Ⅲ. 证法一:首先证明当
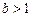 ,
,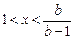 时,恒有
时,恒有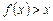 成立.
成立.用数学归纳法证明:
(ⅰ)由Ⅱ知当
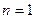 时,在
时,在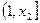 上,
上, 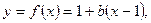
所以
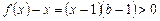 成立
成立(ⅱ)假设
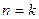 时在
时在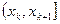 上恒有
上恒有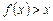 成立.
成立.可得
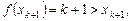
在
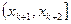 上,
上,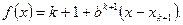
所以
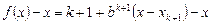
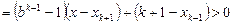 也成立.
也成立.由(ⅰ)与(ⅱ)知,对所有自然数
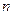 在
在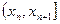 上都有
上都有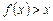 成立.
成立.即
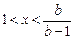 时,恒有
时,恒有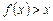 .
.其次,当
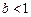 ,仿上述证明,可知当
,仿上述证明,可知当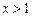 时,恒有
时,恒有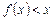 成立.
成立.故函数
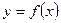 的图像与
的图像与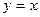 的图像没有横坐标大于1的交点.
的图像没有横坐标大于1的交点. 证法二:首先证明当
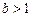 ,
,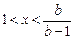 时,恒有
时,恒有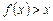 成立.
成立.对任意的
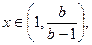 存在
存在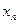 ,使
,使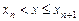 ,此时有
,此时有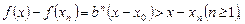
所以
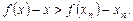
又
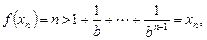 所以
所以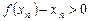 ,
,所以
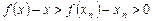 ,即有
,即有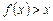 成立.
成立.其次,当
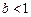 ,仿上述证明,可知当
,仿上述证明,可知当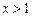 时,恒有
时,恒有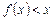 成立.
成立.故函数
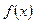 的图像与
的图像与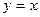 的图像没有横坐标大于1的交点.
的图像没有横坐标大于1的交点. 
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
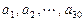 ,其中
,其中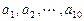 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;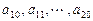 是公差为
是公差为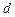 的等差数列;
的等差数列;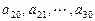 是公差为
是公差为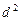 的等差数列(
的等差数列(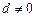 ).
).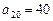 ,求
,求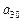 关于
关于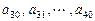 是公差为
是公差为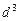 的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?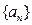 中,
中,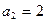 ,前
,前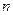 项和为
项和为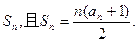
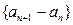 是等差数列,并求出数列
是等差数列,并求出数列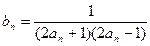 ,数列
,数列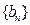 的前
的前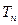 ,求使不等式
,求使不等式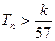 对一切
对一切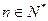 都成立的最大正整数
都成立的最大正整数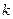 的值。
的值。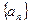 中,
中,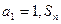 是数列
是数列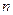 项和,对任意
项和,对任意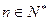 ,均有
,均有 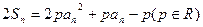 (1).求常数
(1).求常数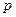 的值;(2)求数列
的值;(2)求数列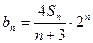 ,求数列
,求数列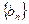 的前
的前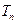 。
。 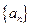 满足
满足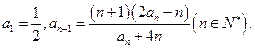
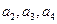 ;(Ⅱ)已知存在实数
;(Ⅱ)已知存在实数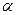 ,使
,使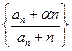 为公差为
为公差为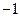 的等差数列,求
的等差数列,求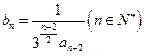 ,数列
,数列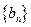 的前
的前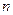 项和为
项和为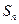 ,求证:
,求证: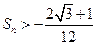 .
.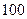 的正整数中,被
的正整数中,被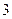 除余
除余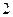 的数的和是 .
的数的和是 .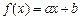 ,其中
,其中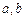 为实数,
为实数,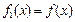 ,
,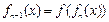 ,
,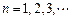 ,若
,若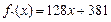 ,则
,则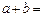 .
.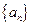 中,
中,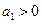 ,且
,且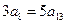 ,则
,则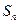 中最大的是 ()
中最大的是 ()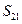
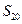
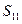
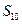
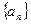 中,
中,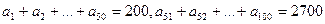 ,
,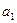 为( )
为( )