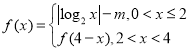题目内容
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)若a=1.解不等式f(x)≤x2﹣1;
(2)若a>0,b>0,c>0.且f(x)的最小值为4﹣b﹣c.求证:![]() .
.
【答案】(1){x|x≤﹣2或x≥1![]() }(2)证明见解析
}(2)证明见解析
【解析】
(1)对绝对值函数进行分段讨论,解不等式即可;
(2)求出![]() 的最小值,得到
的最小值,得到![]() ,利用柯西不等式证明即可.
,利用柯西不等式证明即可.
(1)当a=1时,f(x)=|x﹣1|+|x+2|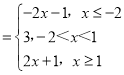 ,
,
当x≤﹣2时,﹣2x﹣1≤x2﹣1,得x2+2x≥0,所以x≤﹣2;
当﹣2<x<1时,3≤x2﹣1,得x2≥4,无解
当x≥1时,由2x+1≤x2﹣1,得x2﹣2x﹣2≥0,得x≥1![]() ,
,
综上,不等式的解集为{x|x≤﹣2或x≥1![]() };
};
(2)证明:
因为f(x)=|x﹣a|+|x+2|≥|x﹣a﹣x﹣2|=|a+2|=a+2=4﹣b﹣c,
得a+b+c=2,
所以![]()
![]() 2,
2,
当且仅当a+b=c=1时成立,
故原命题得证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目