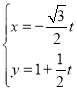题目内容
【题目】已知函数f(x)=lnx﹣ax,其中a为实数.
(1)求出f(x)的单调区间;
(2)在a<1时,是否存在m>1,使得对任意的x∈(1,m),恒有f(x)+a>0,并说明理由.
【答案】(1)答案见解析;(2)在a<1时,存在m>1,使得对任意x∈(1,m)恒有f(x)+a>0。理由见解析。
【解析】
(1)对函数求导,并分a≤0和a>0两种情况讨论。可求出结果;(2)结合(1)将a<1分为a≤0和![]() 两种情况进行讨论即可。
两种情况进行讨论即可。
(1)∵f(x)=lnx﹣ax,
∴ ![]() ,
,
当a≤0时,f'(x)>0恒成立,
函数f(x)在定义域(0,+∞)递增;无减区间
当a>0时,令f'(x)=0,则x=![]() ,
,
当x∈(0,![]() )时,f'(x)>0,函数为增函数,
)时,f'(x)>0,函数为增函数,
当x∈(![]() ,+∞)时,f'(x)<0,函数为减函数。
,+∞)时,f'(x)<0,函数为减函数。
![]()
![]()
(2)在a<1时,存在m>1,使得对任意的x∈(1,m)恒有f(x)+a>0。
理由如下:
由(1)得
当a≤0时,函数f(x)在(1,m)递增,
![]() ,
,
![]() ,
,
![]()
![]()
即f(x)+a>0。
综上可得:在a<1时,存在m>1,使得对任意x∈(1,m)恒有f(x)+a>0。

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
【题目】某学校为了调查学生的学习情况,由每班随机抽取![]() 名学生进行调查,若一班有
名学生进行调查,若一班有![]() 名学生,将每一学生编号从
名学生,将每一学生编号从![]() 到
到![]() ,请从随机数表的第
,请从随机数表的第![]() 行第
行第![]() 、
、![]() 列(下表为随机数表的前
列(下表为随机数表的前![]() 行)开始,依次向右,直到取足样本,则第五个编号为_________.
行)开始,依次向右,直到取足样本,则第五个编号为_________.
7816 | 6514 | 0802 | 6314 | 0702 | 4369 | 9728 | 0198 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
7816 | 6514 | 0802 | 6314 | 0702 | 4369 | 9728 | 0198 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |