题目内容
2. 如图,在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,PC⊥AB,E为PD上一点,且PD=3PE.
如图,在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,PC⊥AB,E为PD上一点,且PD=3PE.(Ⅰ)求异面直线AB与CE所成角的余弦值;
(Ⅱ)求平面PAC与平面ABCD所成的锐二面角的余弦值.
分析 (Ⅰ)建立空间坐标系,利用向量法即可求异面直线AB与CE所成角的余弦值;
(Ⅱ)建立空间坐标系,利用向量法即可求平面PAC与平面ABCD所成的锐二面角的余弦值.
解答 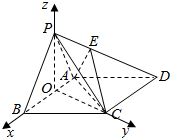 解:(I)取AB的中点O,连接PO,OC
解:(I)取AB的中点O,连接PO,OC
∵△PAB为边长为2的正三角形,
∴PO⊥AB
又∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PO?平面PAB
∴PO⊥平面ABCD,
又∵PC⊥AB,PO∩PC=P,PO,PC?平面POC
∴AB⊥平面POC
又∵OC?平面POC
∴AB⊥OC
以O为坐标原点,建立如图所示的空间坐标系,
则A(-1,0,0),C(0,$\sqrt{3}$,0),P(0,0,$\sqrt{3}$),D(-2,$\sqrt{3}$,0),B(1,0,0),
∵PD=3PE,
∴E($-\frac{2}{3}$,$\frac{\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$)
则$\overrightarrow{AB}$=(2,0,0),$\overrightarrow{CE}$=($-\frac{2}{3}$,-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$),
则|$\overrightarrow{CE}$|=$\frac{2\sqrt{7}}{3}$,
则cos<$\overrightarrow{AB}$,$\overrightarrow{CE}$>=$\frac{\overrightarrow{AB}•\overrightarrow{CE}}{|\overrightarrow{AB}||\overrightarrow{CE}|}$=$\frac{-\frac{4}{3}}{2×\frac{2\sqrt{7}}{3}}$=-$\frac{\sqrt{7}}{7}$,
即异面直线AB与CE所成角的余弦值为$\frac{\sqrt{7}}{7}$.
(2)设平面PAC的法向量为$\overrightarrow{m}$=(x,y,z),
∵$\overrightarrow{AC}$=(1,$\sqrt{3}$,0),$\overrightarrow{CP}$=(0,-$\sqrt{3}$,$\sqrt{3}$),
∴由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AC}=0}\\{\overrightarrow{m}•\overrightarrow{CP}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{x+\sqrt{3}y=0}\\{-\sqrt{3}y+\sqrt{3}z=0}\end{array}\right.$,
令z=1,则y=1,x=$-\sqrt{3}$,
即$\overrightarrow{m}$=($-\sqrt{3}$,1,1),
平面ABCD的法向量为$\overrightarrow{n}$=(0,0,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
故平面PAC与平面ABCD所成的锐二面角的余弦值为$\frac{\sqrt{5}}{5}$.
点评 本题主要考查异面直线所成角的求解,以及二面角的求解,建立空间坐标系,利用向量法是解决二面角的常用方法.考查学生的运算和推理能力.

| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{-1+i}{2}$ | D. | $\frac{-1-i}{2}$ |
| A. | 0 | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,三棱柱 ABC-A1B1C1 中,AA1⊥平面 A1B1C1,AB=AC=AA1=2,AB⊥AC,D 为 AC 中点,点 E 在棱 CC1C上,且 AE⊥平面 A1B1D.
如图,三棱柱 ABC-A1B1C1 中,AA1⊥平面 A1B1C1,AB=AC=AA1=2,AB⊥AC,D 为 AC 中点,点 E 在棱 CC1C上,且 AE⊥平面 A1B1D. 已知点P(1,3),Q(1,2).设过点P的动直线与抛物线y=x2交于A,B两点,直线AQ,BQ与该抛物线的另一交点分别为C,D.记直线AB,CD的斜率分
已知点P(1,3),Q(1,2).设过点P的动直线与抛物线y=x2交于A,B两点,直线AQ,BQ与该抛物线的另一交点分别为C,D.记直线AB,CD的斜率分