题目内容
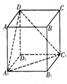
20．
如图，三棱柱 ABC-A1B1C1 中，AA1⊥平面 A1B1C1，AB=AC=AA1=2，AB⊥AC，D 为 AC 中点，点 E 在棱 CC1C上，且 AE⊥平面 A1B1D．（Ⅰ）求 CE 的长；
（Ⅱ）求三棱锥 E-A1BD 的体积．
分析 （Ⅰ）根据线面垂直的性质定理，证明AE⊥A1D，利用D为AC的中点，即可求CE的长；
（Ⅱ）根据锥体的条件公式确定三棱锥的底面积和高即可以求出锥体的体积．
解答 解：（Ⅰ）∵AE⊥平面 A1B1D，
∴AE⊥A1D，
又ACC1A1是边长为2的正方形，D为AC的中点，
故E为CC的中点，∴CE=1； …（6分）
（Ⅱ）∵AA1⊥平面A1B1C1，∴AA1⊥AC，
又AB⊥AC，
∴BA⊥平面ACC1A1．
∴${V}_{E-{A}_{1}BD}$=${V}_{E-{A}_{1}DE}$=$\frac{1}{3}×2×{S}_{△{A}_{1}DE}$=$\frac{2}{3}$×（4-$\frac{1}{2}-1-1$）=1．…（12分）
点评 本题主要考查线面垂直的性质，以及三棱锥的体积的计算，利用等积法转化是解决本题关键．
练习册系列答案
相关题目
某市园林管理处为了了解在某片土地上培育的树苗的生长情况，在树苗种植一年后，从中随机抽取10株，测得它们的高度（单位：cm），并将数据用茎叶图表示（如图），已知x∈[6，9]，且x∈N．
8．设函数f（x）=exsinx-cosx，g（x）=xcosx-$\sqrt{2}$ex（其中e是自然对数的底数），?x1∈[0，$\frac{π}{2}$]，?x2∈[0，$\frac{π}{2}$]，使得不等式f（x1）+g（x2）≥m成立，则实数m的范围（ ）
| A． | （-∞，-1-$\sqrt{2}$] | B． | （-∞，${e}^{\frac{π}{2}}$-$\sqrt{2}$] | C． | （-∞，-1-$\sqrt{2}$${e}^{\frac{π}{2}}$] | D． | （-∞，（-1-$\sqrt{2}$）${e}^{\frac{π}{2}}$] |
某人在5场投篮比赛中得分的茎叶图如图所示，若五场比赛的平均得分为11分，则这五场比赛得分的方差为8．
如图，在四棱锥P-ABCD中，△PAB是边长为2的正三角形，底面ABCD为菱形，且平面PAB⊥平面ABCD，PC⊥AB，E为PD上一点，且PD=3PE．