题目内容
11.设椭圆C的中心在原点,左,右焦点分别为F1,F2,过F1垂直x轴的直线与椭圆相交于A,B两点,|AB|=$\frac{2\sqrt{3}}{3}$,且△F2AB的周长为4$\sqrt{3}$.(1)求椭圆C的方程;
(2)过圆D:x2+y2=4上任一点P作椭圆C的两条切线m,n,直线m,n与圆D的另一交点分别为M,N.
①证明:m⊥n;
②求△MNP面积的最大值.
分析 (1)设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>1),把x=-c代入椭圆的方程可得:$\frac{2{b}^{2}}{a}$=$\frac{2\sqrt{3}}{3}$,由△F2AB的周长为4$\sqrt{3}$,可得4a=4$\sqrt{3}$,解得a,b即可得出.
(2)①设P((x0,y0),则${x}_{0}^{2}+{y}_{0}^{2}$=4.当切线的斜率都存在时,设切线的方程为:y-y0=k(x-x0),代入椭圆的方程可得:(1+3k2)x2+6k(y0-kx0)x+3(y0-kx0)2-3=0,△=0,化为(${x}_{0}^{2}$-3)k2-2kx0y0+${y}_{0}^{2}$-1=0.当${x}_{0}^{2}$-3≠0时,k1k2=-1,可得m⊥n.当${x}_{0}^{2}$-3=0时,也有m⊥n.即可证明.
②由①可得:m⊥n,可得MN为⊙D的直径,因此MN过圆心即原点O.当OP⊥MN时,△MNP面积取得最大值.
解答 解:(1)设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>1),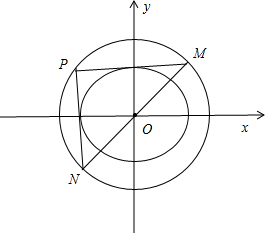
把x=-c代入椭圆的方程可得y=$±\frac{{b}^{2}}{a}$,
∴$\frac{2{b}^{2}}{a}$=$\frac{2\sqrt{3}}{3}$,
∵△F2AB的周长为4$\sqrt{3}$,∴4a=4$\sqrt{3}$,
解得a=$\sqrt{3}$,b2=1,
∴椭圆C的方程为$\frac{{x}^{2}}{3}+{y}^{2}=1$.
(2)①设P((x0,y0),则${x}_{0}^{2}+{y}_{0}^{2}$=4.
当切线的斜率都存在时,设切线的方程为:y-y0=k(x-x0),
代入椭圆的方程可得:(1+3k2)x2+6k(y0-kx0)x+3(y0-kx0)2-3=0,
△=36k2$({y}_{0}-k{x}_{0})^{2}$-12(1+3k2)[$({y}_{0}-k{x}_{0})^{2}$-1]=0,
化为(${x}_{0}^{2}$-3)k2-2kx0y0+${y}_{0}^{2}$-1=0.
当${x}_{0}^{2}$-3≠0时,k1k2=$\frac{{y}_{0}^{2}-1}{{x}_{0}^{2}-3}$=$\frac{4-{x}_{0}^{2}-1}{{x}_{0}^{2}-3}$=-1,∴m⊥n.
当${x}_{0}^{2}$-3=0时,也有m⊥n.
综上可得:m⊥n.
②由①可得:m⊥n,∴MN为⊙D的直径,因此MN过圆心即原点O.
∴当OP⊥MN时,△MNP面积取得最大值$\frac{1}{2}×2×4$=4.
点评 本题考查了椭圆及其圆的标准方程及其性质、直线与椭圆相切问题、三角形面积计算公式,考查了分类讨论思想方法、推理能力与计算能力,属于难题.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | (0,2$\sqrt{3}$) | B. | (-$\frac{1}{2}$,2$\sqrt{3}$) | C. | (0,-2$\sqrt{3}$) | D. | (-$\frac{1}{2}$,-2$\sqrt{3}$) |
 某市园林管理处为了了解在某片土地上培育的树苗的生长情况,在树苗种植一年后,从中随机抽取10株,测得它们的高度(单位:cm),并将数据用茎叶图表示(如图),已知x∈[6,9],且x∈N.
某市园林管理处为了了解在某片土地上培育的树苗的生长情况,在树苗种植一年后,从中随机抽取10株,测得它们的高度(单位:cm),并将数据用茎叶图表示(如图),已知x∈[6,9],且x∈N.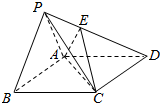 如图,在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,PC⊥AB,E为PD上一点,且PD=3PE.
如图,在四棱锥P-ABCD中,△PAB是边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,PC⊥AB,E为PD上一点,且PD=3PE.